서울대 기계공학과의 최고 인기수업은 무엇일까요?
그 수업에선 어떤 걸 배울까요? 어쩌면 나도 이해해 볼 수 있지 않을까요?
서울대 기계공학과 최고의 수업, 로봇공학입문을 소개해드립니다.
0. 전공백서: 로봇공학입문
이번 전공백서에서는 서울대학교 기계공학과 최고의 명강의로 꼽히는 로봇공학입문 강의를 소개해드리고자 합니다. 로봇공학입문(이하 로공입)은 수학적으로 내용이 많이 어려워 서울대 학생들도 이해에 많은 어려움을 겪는 과목입니다. 그래서 내용을 구체적으로 다루기보단 로공입이 어떠한 느낌의 과목인지 느끼고, 기계공학과에서는 로봇을 어떻게 바라보는지 고등학생분들이 이해할 수 있도록 서술하고자 합니다.
로공입 강의는 서울대 기계과의 자랑 박종우 교수님께서 3학년을 대상으로 개설하시는 강의입니다. 강의내용은 박종우 교수님께서 직접 1995년 논문에서 로봇의 움직임을 깔끔하게 정리하신 내용을 기반으로 짜여있습니다. 현재 교수님은 ICRA(IEEE International Conference on Robotics and Automation)이라는 국제로봇학회의 학회장을 맡고 계십니다. 로공입은 전공선택 과목으로, 그 명성 때문에 대부분의 기계과 학생들이 듣는 과목입니다. 교수님의 강의를 듣고자 서울대로 교환학생/유학을 온 외국인 학생들도 있을 정도입니다. 4대 역학이 기계공학을 전반적으로 이해하는 데에 기반이 되었다면, 로공입은 기계공학 최고인기 분야 중 하나인 로보틱스를 소개해드릴 수 있는 과목이기에 전공백서에서 작성하게 되었습니다.
1. 과목개요
로공입은 100% 이론 수업으로 강의가 진행되며, 정규 수업 시간 이외에 주에 1시간씩 조교님과 함께 강의 복습 + 연습문제 풀이 + 질의응답을 하는 시간이 있습니다. 강의내용이 워낙 어렵기에 연습 세션은 많은 수강생들에게 큰 도움이 됩니다. 또한 교수님은 별도의 ppt나 교재를 사용하지 않고, 커다란 칠판에 판서를 하며 강의를 진행하십니다. (이때 간지가 철철 넘쳐흐릅니다.)
성적은 시험 성적을 기반으로 매겨집니다. 로공입 시험의 특징은 성적이 공부량에 비례하지만은 않는다는 것입니다. 대부분의 다른 강의와는 다르게 기출문제들과 문제가 겹치는 법이 절대 없고, 매번 조교님들이 새로운 문제를 창조해내십니다. 문제 난이도가 상당히 높고, 수업내용과는 별개로 수학적 사고력 및 계산속도가 고득점에 유리합니다.
로공입에서 다루는 로봇은 link와 joint의 결합으로 이루어진 물체입니다. 여기서 joint는 로봇의 link를 움직이는 관절이고, link는 joint에 의해 움직여지는 로봇의 뼈라고 이해하시면 됩니다. “로봇에도 감정이 존재할까?”, “로봇의 디자인을 어떻게 해야 할까?” 등의 인문학적, 예술적인 관점에선 전혀 접근하지 않습니다. 또한, “로봇의 재질을 어떻게 바꾸어야 할까?”, “로봇이 고장 나지 않는 재질은 무엇일까?” 등의 소재나 고체 역학적인 관점에서도 전혀 접근하지 않습니다. 로공입에서 관심 있는 것은 오로지 로봇의 동적인 움직임입니다. 그래서 로공입에서 다루는 로봇의 그림들은 사실 이쁘진 않습니다^^;; 오로지 뼈다귀와 관절로만 표현이 됩니다.
로공입에서 다루는 내용은 DoF, Grasping, Forward/Inverse Kinematics, Path Planning입니다. 해당 내용에 대해서 간략하게 소개해드리도록 하겠습니다.
2. DoF(Degrees of Freedom, 자유도)
로공입에서 처음 배우는 것은 로봇의 DoF(Degrees of Freedom), 즉 자유도를 계산하는 것입니다. 자유도란 무엇일까요? 다음과 같은 예시를 생각해봅시다.
임의의 세 숫자 a, b, c를 뽑는 경우를 생각해볼까요? a, b, c는 자유롭게 막 뽑을 수 있기 때문에, 이 경우는 a, b, c를 뽑는 자유도는 3이라고 할 수 있습니다.
이제, a, b, c의 합이 1이 된다는 다음과 같은 조건 하에 a, b, c를 뽑는다고 생각해봅시다.
a+b+c=1
이 경우, a, b는 마음대로 고를 수 있지만, 그 경우 c가 자동으로 결정됩니다. 가령 a=5.6, b=0.7로 두면 c는 -5.3으로 자동으로 결정되죠. 반대로 a, c를 마음대로 고르면 b가 자동으로 결정됩니다. 이런 경우 a, b, c를 자유롭게 뽑을 수 있는 개수는 2개고, a, b, c를 뽑는 자유도는 2라고 할 수 있습니다.
로봇의 예시로 돌아가 볼까요? 다음과 같은 그림을 생각해봅시다.
위의 그림은 4-bar linkage라고 하는 구조입니다. 1개의 주황색과 3개의 노란색 link와 그들을 연결하는 4개의 점 같은 joint들이 있죠. 로공입에서 그리는 로봇은 안타깝게도 다 위와 같은 심미성이 떨어지는 그림들입니다. 우리는 여기서 4개의 관절을 돌리면서 link 사이의 각도를 바꿀 수 있습니다. 그러면 해당 구조의 자유도는 4일까요?
생각을 해봅시다. 왼쪽 아래의 joint를 돌리면, 위의 노란 link가 돌아갈 것이고, 그러면 연결된 다른 joint들과 link들도 맞추어서 돌아갈 것처럼 보이지 않나요? 과연 2개의 joint를 동시에 원하는대로 돌릴 수 있을까요? 한쪽 joint의 각도를 원하는 값으로 고정하면, 다른 joint들은 link의 길이에 따라 자동적으로 각도가 정해질 것이고, 우리가 원하는 각으로 임의로 조절을 못 합니다. 결국, 해당 구조에 자유도는 1인 것입니다.
로봇을 설계할 때 해당 구조의 자유도를 아는 것은 매우 중요합니다. 가령, 위와 같은 4-bar linkage에서 2개의 joint의 각도를 동시에 제어하려고 하면 어떻게 될까요? 아마 joint들끼리 각자 원하는 각도로 돌아가려고 힘겨루기를 하다가 로봇이 고장 날 것입니다. joint들 중 1개만 제어해야 안전하게 운영이 되겠죠. 그래서 로봇의 자유도를 구하는 것은 중요합니다. 그러나 더 복잡한 구조들에서 자유도를 직관적으로 알아내기는 어렵습니다. 가령 다음과 같은 예시를 볼까요?
위와 같은 구조만 되어도 자유도를 구하기엔 매우 어렵습니다. 심지어 3차원으로 구조가 확장되면 더 어렵지요.
해당 구조들의 DOF를 잘 계산할 수 있는 방법은 없을까요? 다행히 Gruebler’s Formula라는 공식을 통해 쉽게 계산이 가능합니다.
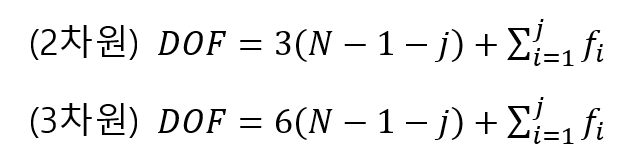
여기서 N은 link의 개수, J는 joint의 개수, fi는 각 joint에 해당하는 DoF입니다. 공식을 이해하실 필요는 없습니다! 다만 link, joint의 개수를 세는 것만으로도 DoF를 빠르게 계산하는 방법이 있다 정도로 알아두시면 되겠습니다!
Gruebler’s formula를 활용하여 DoF를 계산하는 것은 매 중간고사 1번 문제로 나오게 됩니다. 한번은 교수님이 팔에 깁스를 하신채로 수업에 오신 적이 있었습니다. 그리고 “내 팔의 DoF를 잃었다”라는 농담을 던지신 적이 있었죠^^ Gruebler’s formula는 그러나 link의 길이와 위치 배치에 따라 종종 맞지 않는 경우가 있습니다. 자세한 내용은 어려우니, 완벽하지만은 않다~ 정도로만 알아두시면 되겠습니다. (로공입 강의에서도 그 정도로 넘어갑니다)
3. Grasping
여러분은 ‘로봇’하면 어떠한 역할을 하는 로봇들이 떠오르나요? 저는 사실 춤추는 로봇들이 제일 먼저 떠올랐습니다. 현대에서 인수한 Boston Dynamics라는 회사에서는 BTS와 함께 춤추는 로봇들의 영상을 공개하기도 했죠. 그러나 상업적으로 활용성이 가장 높은 로봇들은 사람의 형상보다는 단순한 팔 모양의 로봇이 많습니다. 특히 공장에서 물체를 집고 운반하는 데에 로봇들이 많이 쓰이죠. 여기서 로봇이 물체를 집는 문제는 생각만큼 단순한 문제가 아닙니다. 우리는 손가락과 손목의 관절을 활용하고 손가락에 들어가는 힘을 조절하지만, 매끈매끈한 로봇이 순간순간 물체를 드는 감각을 센싱하고, 각 link의 힘을 적절하게 조절해서 물체를 드는 것은 매우 어렵습니다. 이러한 로봇의 물체를 드는 Grasping 문제는 현재까지도 연구가 진행 중이기도 합니다. 로공입에서는 고전적인, 그리고 수학적인 방식으로 grasping 문제를 분석하게 됩니다.
해당 그림은 제가 수업을 들었을 당시 필기했던 자료입니다. 다음과 같은 액자를 드는 경우를 생각해봅시다. 4개의 손가락을 파란색 점들과 같이 각 변의 가운데에 두고 집는 경우와 빨간색 점들과 같이 비대칭적인 위치에 두고 잡는 경우를 생각해봅시다. 이때 어떠한 구조가 더 안정적일까요? 저는 수업 시간에 파란색이라고 대답을 했습니다. 뭔가 대칭적인 게 안정적일 것 같다는 무의식이 있었죠.
그러나 파란색과 같이 대칭적인 위치에서 잡게 되면 액자를 시계, 반시계 방향으로 흔들었을 때 다시 원래 위치로 돌아오도록 제어가 되지 않습니다. 손가락의 힘을 줄이거나 늘려도 액자를 반대 방향으로 돌리지 못합니다. 반면에 빨간색 손가락은 액자를 시계방향으로 돌리는 손가락과 반대 방향으로 돌리는 손가락이 모두 존재합니다. 가령 위쪽 변에 있는 손가락은 액자를 시계방향으로 돌리고, 오른쪽 변에 있는 손가락은 반시계 방향으로 돌리죠. 그래서 해당 손가락에 가하는 힘의 세기를 조절해 액자를 원래대로 돌려놓을 수 있습니다.
이와 같은 논의를 수학적으로 다룰 수 있습니다. 각각의 손가락이 작용하는 가로방향 힘, 세로방향 힘, 그리고 시계/반시계 방향 힘을 각각 계산할 수 있죠. 이 3개의 값을 모아 하나의 세트로 묶으면, 다음과 같은 벡터의 형태로 바꿀 수 있습니다.
[fxfymz](fx는가로방향힘, fy는세로방향힘, mz는회전힘) [f_x \quad f_y \quad m_z](f_x는 가로방향 힘, \ f_y 는 세로방향 힘, \ m_z는 회전힘)
이때, 우리는 위와 같은 벡터 4개를 적절히 양수배하여 더해 어떠한 외부의 자극을 상쇄할 수 있어야 합니다. 가령 위의 예시에서 파란 손가락들은 모두 액자에 회전 힘을 못 주고, 대신 각각 x, y 방향 양수, 음수의 힘을 주게 됩니다. 즉 벡터로 쓰면 다음과 같죠.
그렇다면 위의 손가락들에 각각 양수배의 숫자 a, b, c, d를 곱해서 더하면 다음과 같은 벡터가 될 것입니다.
양수의 x 방향 힘이 오면 c를 키우고, 음수의 y 방향 힘이 오면 b를 키우는 등으로 외부의 힘을 합해서 0으로 만들 수 있겠죠? 그러나 외부에서 액자를 흔드는 힘이 왔을 때, 파란 손가락들은 액자를 돌릴 수 없어 대처가 불가능합니다. 좋은 grasping 설계가 아니겠죠.
이와 같은 논의를 확장하면, 결국 4개의 벡터들이 만드는 “convex hull”이 모든 3차원 공간을 포함하느냐?라는 수학적인 용어로 표현이 가능합니다. 해당 문제는 선형대수학에 나오는 “Gauss elimination”을 이용하여 단위행렬을 만들고 남은 4번째 벡터의 모든 원소가 음수인가? 라는 문제로 귀결되기도 합니다. 무슨 소린지 모르겠다면 지극히 정상입니다.
grasping 문제는 더 확장하여 손가락에 마찰력을 줄 수 있는 경우에 대해서 논하기 하고, Nguyen’s theorem을 적용하여 손가락이 집는 위치에 원뿔을 그려 해석하기도 합니다. 수학적으로 너무 깊어지기에, 해당 사항이 있다는 것만 알려드리고, 또 선형대수학의 개념들이 grasping problem 이해에 도움이 된다는 점까지만 설명을 드리고 마무리하려 합니다.
사실 로공입에서 다루는 grasping 문제의 해결법은 앞서 언급한 것처럼 고전적이고, 수학적입니다. 실제 로봇 연구에는 로봇의 손가락 소재를 개선하거나, 강화학습 등의 다른 방법으로 grasping 문제를 해결하곤 합니다. 로공입에서의 관점은 가장 수학적으로 아름답고, 직관적인 해석을 준다는 데에 그 의의가 있습니다. Grasping 문제는 중간고사 2번 문제로 단골 출제되며, 보통 4문제 중에 난이도가 제일 낮습니다.
4. Forward Kinematics
Grasping 이후엔 Forward kinematics를 설명하는 데에 많은 시간이 할애됩니다. Forward kinematics란 무엇일까요? 우선 다시 한번 로봇의 grasping 문제를 생각해봅시다.
우리가 실제로 어떠한 물체를 잡기 위해선 로봇에 달려있는 joint들의 각도를 조정하여 물체의 위치에 로봇손을 갖다 놓아야 합니다. 또한 로봇 손의 방향 역시 위에서 아래를 보는 방향, 혹은 왼쪽에서 오른쪽을 보는 방향 등 적절한 방향을 향하도록 설정해야 합니다. 그러나 로봇엔 여러 개의 joint와 link가 복합하게 연결되어 있으므로, joint의 각도가 변함에 따른 로봇손의 위치와 각도를 직관적으로 알기는 어렵습니다. 예시를 하나 살펴볼까요?
위의 그림은 로공입 18년도 중간고사 문제 중 하나입니다. 여기서 원통은 joint, 작대기는 link, {T} 좌표계가 부착된 곳이 로봇손입니다. 로봇팔을 인형뽑기 기계라고 생각해봅시다. 우리가 각 joint들의 각도와 길이를 어떻게 조작을 해야 원하는 인형에 딱 도착할 수 있는지, 또 그 방향이 위에서 아래를 똑바로 바라보는 방향일지 알아내는 것은 어렵습니다. 혹은 각 각도와 길이를 알고 있을 때 로봇손의 위치와 방향을 계산하는 것 역시 어렵습니다.
joint의 각도/길이 데이터를 알고 있을 때 로봇손의 위치를 계산하는 문제를 Forward kinematics라고 하고, 원하는 로봇손의 위치와 방향에 해당하는 joint의 값을 역으로 계산하는 문제를 inverse kinematics라고 합니다. 두 문제 모두 어려운 문제지만, 상대적으로 inverse kinematics가 더 어렵습니다. 그리고 인트로에서 잠깐 언급한 박종우 교수님의 논문은 forward kinematics 문제를 푸는 새로운 방법을 제시한 논문입니다.
제가 이전에 작성한 4대 역학 소개 전공백서를 읽으셨던 분들 중 동역학 부분을 기억하시는 분이 계실까요? 당시 동역학에서 우리는 “관점의 차이” 및 이 관점의 차이를 연결하는 방법에 대해 잠깐 다뤘었습니다. 로공입의 forward kinematics에서도 같은 논의를 이어 나갑니다. 가령 위의 인형 뽑기 그림을 다시 한번 살펴봅시다. 우리가 theta_1을 회전했을 때 로봇 손의 위치와 방향이 어떻게 변화하는지 아는 것은 어렵습니다. 그러나 theta_6과 로봇손과의 관계는 너무 쉽죠. theta_6이 돌아간 만큼 로봇손이 돌아갈 것입니다. 또한, 5번 joint와 6번 joint사이의 관계는 쉽습니다. joint5가 늘어난 길이만큼 joint6의 위치가 변할 것입니다. joint6의 변화하는 위치를 그림에서 보이는 {S}좌표계에서 서술하기는 어렵지만, joint5의 관점에서는 항상 일정하죠. 이처럼 연속한 joint들 사이의 관계를 순차적으로 적용해나가면, 각각의 joint 값이 로봇손의 위치와 방향에 어떠한 영향을 주는지 알 수 있습니다.
물론 이와 같은 아이디어를 알았다고 해서 바로 계산이 가능한 것은 아닙니다. theta5가 1m 늘어났다고 해서 그것이 위의 그림에서 보이는 것처럼 -z 방향으로 1m 이동한 것은 아니죠. theta1~4의 값에 따라 theta5가 늘어난 길이는 어떠한 방향일지 모르는 것입니다. 다만, 우리가 아는 것은 joint5의 관점에서 joint 방향으로 1m 이동했다는 것뿐이죠. 그러면 이것이 어떤 방향인지는 어떻게 알 수 있을까요?
안타깝게도 이 내용을 설명하는 것은 수학적으로 더 깊게 들어가야 합니다. 박종우 교수님의 논문 내용을 본격적으로 설명하는 것이 되고, 완전한 이해를 위해선 수학적 배경이 많이 필요합니다. 선형대수학의 기저 변환 및 Special orthogonal group, Special Euclidean group의 성질에 대한 이해가 필요합니다. 실제로 많은 기계과 학생들은 해당 배경지식이 없는 상태로 로공입 강의를 수강하게 되고, 흐름 이해에 많은 어려움을 겪게 됩니다. 본 전공백서에서도 해당 내용을 깊게 다룰 순 없습니다. 다만, 윗 문단에서 쓴 것과 같이 이웃한 두 joint 사이의 관계는 상대적으로 쉽게 표현되고, 이를 연쇄적으로 적용한다는 아이디어만 소개하도록 하겠습니다. 이 joint 사이의 관계는 매우 특별한 성질을 가진 "행렬"로 표현이 가능하며, 이러한 행렬들을 쭉 곱하게 되면 우리가 궁극적으로 원하는 로봇손의 위치와 방향을 계산할 수 있습니다.
이러한 joint들 사이의 관계를 "행렬"로서 표현하는 방법에는 여러 가지가 있습니다. 이전부터 많이 사용된 방법이고, 또 현재 많은 상업 로봇에서 사용되는 방법은 Denavit-Hartenberg Representation을 사용하는 방법입니다. 그러나 해당 방법은 다소 번거로운 준비작업이 필요하며, joint 사이의 모든 관계를 표현하지는 못한다는 단점이 있습니다.
이를 보완하기 위해 나온 방법이 바로 박종우 교수님께서 직접 개발하신 방법입니다. 역시 joint들 사이의 관계를 행렬로써 표현하는 방법인데, 지수함수를 활용합니다. 바로, e의 행렬 제곱을 계산하는 것이죠. 행렬 자체도 어려운데, 행렬을 제곱에 넣다니… 제정신이 아니군요. Taylor 전개와 Cayley-Hamilton 정리들의 수학적인 기법을 활용하면 e의 행렬 제곱이 깔끔하게 계산됩니다. 교수님의 이 방법을 활용하면 계산은 더 복잡하지만 Denavit-Hartenberg 방법에 비해 더 직관적으로 행렬표현이 가능하며, 표현범위도 더 넓습니다. 어차피 계산은 이제 컴퓨터가 다 하기 때문에, e의 행렬 제곱을 활용한 박종우 교수님의 방법이 더 유용하게 됐습니다. 이 방법을 사용하여 forward kinematics뿐만 아니라, 각 joint의 각속도와 속도들 사이의 관계 역시 구할 수 있습니다. 물론 이 과정에는 더 복잡한 행렬계산이 가미됩니다. 또, 각 joint에 작용하는 돌림힘(토크)와 힘까지 연결 지어 계산이 가능해집니다. 즉, joint와 link로 이루어진 로봇에서 다룰 수 있는 위치, 속도, 힘, 토크 등 모든 동역학적 성분이 분석 가능합니다.
위의 내용이 다소 어렵게 느껴졌을까 두렵네요. 서울대생들도 1학기 동안 배워도 어려워하는 내용을 고등학생이 간단한 줄글을 읽고 이해하는 것은 당연히 어려울 것입니다. joint 각도를 설정함에 따른 로봇손의 위치와 방향을 계산하는 방법을 배우고, 그 과정에서 행렬과 선형대수학이 사용된다! 정도로 이해해주시면 될 것 같습니다 :)
5. Inverse kinematics
앞서 설명한 것처럼 inverse kinematics는 역으로 원하는 로봇손의 위치와 방향을 찾기 위해 설정해야 하는 joint의 각도와 길이를 구하는 과정입니다. Forward kinematics에서 이미 식은 구해놨으므로, forward kinematics에서 구한 방정식을 푸는 과정이라고 볼 수도 있죠. 다만 문제는 방정식의 형태가 우리가 쉽게 풀 수 있는 형태가 아니라, 행렬들의 곱으로 이루어진 방정식이라는 점입니다. 간단한 경우 방정식을 풀 수 있지만, 대부분의 경우 방정식을 푸는 확실한 방법이 정해져 있지는 않습니다. 매번 식의 형태에 따라 방정식을 푸는 방법을 찾아가야 합니다. 상업적으로 많이 쓰이는 로봇(6R PUMA Arm, Stanfor-Type Arm 등)은 inverse kinematics의 일반해가 구해져 있습니다. 그러나, 다른 다양한 로봇이 생길 수 있으므로, 다른 접근법이 필요합니다.
과거와 대비해서 우리에겐 아주 강력한 무기가 생겼습니다. 바로 컴퓨터죠. 컴퓨터가 행렬로 된 연립방정식을 눈치껏 적절한 치환과 대입법을 찾아 계산할 수는 없습니다. 그러나, 컴퓨터는 대신에 매우 빠른 사칙연산과 미분을 할 수 있는 능력을 갖추고 있습니다. 우리는 inverse kinematics 문제를 컴퓨터를 활용하여 수치적으로 풀어낼 수 있습니다. 결국 inverse kinematics 문제는 연립방정식을 푸는 것입니다. 비단 inverse kinematics 문제뿐만 아니라, 일반적인 연립방정식을 수치적으로 컴퓨터를 활용해서 푸는 방법을 배웁니다.
우리는 연립방정식을 풀기 위해 Newton-Raphson 방법을 사용합니다. Newton-Raphson법은 미분을 활용하여 방정식의 해를 구하는 방법입니다.
Newton-Raphson 방법의 핵심은 위 그림과 같습니다. 우선, 연립방정식의 좌, 우변을 적당히 이항시켜 한쪽으로 몰아 꼴의 식으로 만듭니다. 물론, 연립방정식의 변수는 여러개가 있을 수 있기에 θ는 여러개의 변수들을 모아 만든 벡터 형태가 될 것입니다. f(θ)는 여러 개의 변수들로 이루어진 여러 개의 연립방정식을 한 번에 모아놓은 형태라고 생각하면 됩니다. 우리가 원하는 연립방정식의 해는 f(θ)=0을 만족하는 해입니다. 우리가 원하는 해를 θ_d라고 합시다. 우리는 θ_d를 모르기에, 임의의 θ_0을 잡아서 그때의 함숫값을 계산합니다. 또한, 그때 함수의 미분을 계산합니다. 그러면, 우리는 θ_0에서의 접선의 방정식을 구할 수 있고, 접선의 x 절편을 구할 수 있습니다. 이는 θ_1이 됩니다. 또, θ_1에서 비슷하게 접선의 x 절편을 구해 θ_2라고 둡시다. 위의 그림에서 볼 수 있다시피, 위 과정을 반복함에 따라 θ_0, 1, 2들은 θ_d를 향해 다가가고 있고, 위 과정을 충분히 반복하면 우리는 연립방정식의 해를 구할 수 있습니다. 물론 엄청난 수치계산이 필요하기에 컴퓨터를 통해서만 가능한 방법이죠.
어? 그런데 위의 그래프는 θ의 변수가 1개일 때의 그래프 아닌가요? 변수가 여러 개고 연립방정식도 여러 개의 식으로 구성되면 미분은 어떻게 계산되고 그래프에서는 어떻게 계산될까요? 위 의문이 드셨다면 아주 훌륭히 따라오고 계신 겁니다. 내용은 역시 수준이 높아 자세히는 설명해 드리진 않겠습니다. 다만, 변수가 여러 개고 식이 여러 개 있더라도 같은 방법으로 확장이 가능하고, Jacobian이라는 값을 활용하여 미분을 대체할 수 있습니다. 자세한 내용이 궁금하신 분은 벡터 미적분학을 공부하시면 되겠습니다.
위 방법은 사실 θ_0의 위치에 따라 해를 구할 수도 있고, 해가 아닌 곳에서 발산할 수도 있습니다. 따라서 초기값을 잘 잡는 게 중요합니다.
Inverse kinematics의 또 다른 문제는 해가 유일하지 않을 수 있다는 것입니다. 특히, joint의 개수가 늘어남에 따라 원하는 joint의 위치와 방향을 나타내는 joint의 값들은 무수히 많아질 수 있습니다. 이를 중 어떠한 값을 선택하더라도 큰 상관은 없습니다. 다만, 컴퓨터가 로봇 joint를 알아서 계산하도록 하는 알고리즘을 설계할 때는 그러한 해들 중 어떤 것을 고를지를 명확히 지정을 해줘야겠죠. 컴퓨터는 임의 판단을 하지 못합니다. 이러한 문제와 연결하여 박종우 교수님은 최적화 문제를 소개하십니다.
최적화 문제는 제약조건을 만족하는 상황 속에서 원하는 목적함수를 최대화, 최소화하는 문제입니다. 가령 다음과 같은 예시들이 있을 수 있죠.

여기서 min은 minimize의 약자로 목적함수를 최소화하고 싶다는 의미입니다. s.t.는 subject to의 약자로 다음과 같은 제약조건을 만족해야 한다는 것이죠. 즉, 두 수의 합이 1이라는 조건 하에서 두 수의 제곱의 합을 최소화하고 싶다는 것입니다. 위 문제는 이차함수를 배운 학생이라면 쉽게 해결할 수 있을 겁니다. 0.5가 최소해가 되겠죠.
최적화 문제는 정말 넓고 많은 분야에서 활용됩니다. 가령 택배를 운송할 때 모든 지역에 배달하되(제약조건) 운송 시간 혹은 기름값을 최소화하고 싶을 수 있습니다. 주식에 투자할 때 일정 수준 이상의 수익률을 내도록 하되, 위험성을 최소화하고 싶을 수 있습니다. 요새 많이 떠오르는 분야인 AI, 딥러닝 등도 모두 최적화 문제를 푸는 과정입니다. 서울대학교의 산업공학과나 수리과학부 등에는 최적화 문제만을 전문적으로 다루는 과목들도 많이 있습니다. 로공입에서는 유명한 최적화 문제 중 하나인 최소제곱법을 예제로써 학습합니다. 역시 기본적인 행렬계산 및 벡터 미분의 개념이 필요합니다.

Inverse kinematics에선 그러면 최적화 문제를 어떻게 사용할까요? 원하는 손의 위치와 방향을 만드는 joint의 값이 여러 개라면 그중 하나를 다음과 같은 최적화 문제를 통해 풀 수 있을 것입니다.

Inverse kinematics의 해 혹은 다른 목적함수를 사용하여 다른 값을 최소화하는 방법도 사용될 수 있습니다.
6. Motion Planning
로공입에서 마지막으로 배우는 것은 motion planning입니다. 우리가 inverse kinematics를 통해서 원하는 곳으로 로봇손을 보내기 위한 joint 값을 다 구했다고 가정합시다. 그렇지만, 원하는 지점까지 로봇손을 보내는 경로엔 여러 가지가 있을 겁니다. 그러한 경로를 설정하는 여러 방법에 대해 학습하게 됩니다.
첫 번째로는 Lagrange interpolation이라는 방법입니다. 로봇이 지나가길 원하는 점 N개와 그 점을 지나가길 원하는 시간을 설정하면, 정해진 시간에 그 점들을 지나면서 움직일 수 있습니다. 즉, (t1,x1),(t2,x2), ... ,(tN,xN)을 지나게 하는 식을 하나 찾아야 하고, 우리는 다음과 같은 N-1차 방정식 f(t)를 활용할 수 있습니다.

위 식에 점들을 넣어 연립방정식을 풀면 f(t)를 쉽게 구할 수 있습니다. 위 방법은 정해진 점들을 원하는 시간대에 모두 통과하게 하지만, 그만큼 길이 구불구불해지고 진동이 많다는 단점이 있습니다.
두 번째는 cubic spline이라는 방법입니다. 위와 똑같이 N개의 점을 잡아 (t1,x1),(t2,x2), ... ,(tN,xN)을 지나가도록 하되, 이를 잇는 하나의 함수를 f(t)를 찾지 않습니다. 대신 이웃한 두 점 사이를 지나가는 3차 함수를 계산하여 N-1개의 3차 함수를 이어 붙여 경로를 만듭니다. 이 경우 훨씬 부드러운 경로를 만들 수 있습니다.
굳이 N개의 점을 도시하지 않는 경로 설정법도 있습니다. 세 번째 방법은 Bezier curve를 활용하는 방법입니다. 이 방법은 로봇이 지나갈 점이 아닌, 장애물 등이 없어 로봇이 지나가는 것이 허용된 구간을 점으로 찍어줍니다. Bezier curve는 이 구역의 꼭짓점들의 좌표를 이웃한 점들끼리 내분하고, 내분해서 나온 점들을 다시 내분하는 등의 과정을 통해 얻은 점들의 집합입니다. 이 curve는 아래 그림과 같이 정해진 구역을 매끄럽게 통과할 수 있게 만듭니다. 장애물로 인해 갈 수 있는 곳이 제한적일 때 더 유용한 방법입니다.
4번째 방법은 potential field method입니다. 이 방법은 일종의 스키장을 만드는 방법입니다. 우리의 시작점을 높은 언덕으로 두고, 도착점을 제일 낮은 골짜기로 둡시다. 그리고, 지나가면 안 되는 장애물을 높은 언덕들로 만들어놓습니다. 출발점에서 스키를 타고 내려가면 장애물을 거치지 않고 제일 낮은 도착점으로 내려가겠죠? 위 방법을 함수로 만든 것이 potential field method입니다. 출발점과 장애물에선 높은 값, 도착점에선 낮은 값, 그 사이는 매끄럽게 이어지게 하는 함수를 설정합니다. 해당 함수의 미분값은 기울기가 될 것이고, 미분값이 가장 낮아지는 방향으로 위치를 조금씩 이동시키면 도착점에 도착할 것입니다. 이 방법은 머신러닝에도 활용되는 gradient descent 방법과 유사합니다.
이와 같은 다양한 경로 설계 방법이 있고, 각각의 장단점이 있습니다. 주어진 상황에 따라서 적절한 방법을 선택하여 로봇의 이동 경로를 설정할 수 있습니다.
7. 맺으며
로공입에서 배운 내용들을 다시 한번 되새겨볼까요? 우리는 로봇을 처음 보고 총 몇 개의 joint를 제어해야 하는지 DoF 분석을 통해 확인할 수 있습니다. 그런 다음 forward kinematics를 통해 해당 joint들의 값 변화에 따른 로봇손의 위치변화를 식으로 표현할 수 있습니다. 이 식을 이용해 inverse kinematics를 적용하면 결국 우리가 입력해야 하는 joint 값을 얻어낼 수 있습니다. Path planning을 통해 로봇이 움직이는 과정까지 설계가 가능합니다. 마지막으로 Grasping을 고려하여 안정적으로 로봇이 물체를 들어 올릴 수 있도록 할 수 있게 됐습니다!
그러나 우리가 로봇을 조작할 때마다 위와 같은 복잡한 계산을 거쳐야 할까요? 실제 사용화된 로봇들에는 위와 같은 계산들이 자동화돼있습니다. 우리는 로봇이 가길 원하는 좌표 및 방향만 입력하게 되면, 로봇은 경로 설정까지 하여 알아서 이동합니다. 복잡한 행렬계산을 직접 할 이유가 없는 것이죠.
그렇다면 우리는 위와 같은 과목을 왜 공부했을까요?
축구선수들은 축구공을 찰 때 속도와 가속도, 공기저항 등에 대해서 고려하지 않습니다. 몸으로 훈련하고 감으로 찰 뿐이죠. 수영선수들 역시 열심히 몸으로 훈련할 뿐 유체역학에 대해 잘 모릅니다. 그러나, 더 강력한 축구공을 설계하는 사람들, 더 좋은 수영복을 설계하는 사람들은 그 원리에 대해 알고 있어야 합니다.
상용화된 소프트웨어를 활용하여 로봇을 조작하는 것은 누구나 할 수 있습니다. 어린 초등학생들도 방법만 익히면 금방 할 수 있죠. 그러나 완벽한 로봇은 없습니다. 로봇이 이동할 때 오차를 더 줄이고, grasping을 더 안정적으로 하고, 실시간으로 바뀌는 외부상황 속에서 경로를 수정해야 할 수도 있습니다. 사람과 협업하는 로봇이 만들어질 수도 있고, 드론 등 공중에 있는 로봇은 더더욱 외부 공기흐름 데이터를 받아들이고 이를 반영하여 경로를 수정해야 할 것입니다. 이러한 부분들엔 더 많은 개선이 앞으로도 이루어져야 합니다. 이러한 연구를 진행할 때 forward / inverse kinematics에 대한 이해가 없이 연구가 진행될 수 있을까요? 절대 불가능합니다. 그것이 우리가 로공입 수업을 공부하는 이유입니다.
그러나 로봇의 경로 설정에 대한 연구가 이미 많은 부분 진행됐다는 것 또한 사실입니다. 최근 로봇 연구는 위에서 다룬 행렬계산을 기반으로 수정을 거듭하는 연구보다는 다른 방법을 활용한 연구가 많습니다. 많은 시뮬레이션과 실험을 통해 데이터를 쌓고, 이를 기반으로 강화학습 등 컴퓨터공학 분야에서 발전이 이루어진 내용들을 적용하는 경우가 많습니다. 또한, 로봇에 카메라를 부착하고 이를 컴퓨터를 통해 분석하는 연구가 늘어나고 있죠. 이러한 트렌드에 맞추어 미래의 로봇공학자를 지망하는 학생들은 기본적인 컴퓨터공학 지식이 필요할 것입니다. 그렇다고 하더라도 로공입에서 다룬 내용들은 여전히 로봇 연구에 기반이 됩니다.
로공입은 4대 역학을 비롯한 기계공학과의 다른 과목들과 성격이 사뭇 다릅니다. 고전적인 역학은 오래전에 정립되고 완성된 학문이라면, 로공입의 수업내용은 최근에도 활발히 연구되고 있는 분야입니다. forward / inverse kinematics는 교수님이 고작 20여 년 전 출판한 논문에 있는 내용입니다. potential field method는 최근에 각광받기 시작한 알고리즘이며, 실제 로봇 연구에 널리 활용되는 강화학습 역시 최근 내용입니다. 4대 역학의 결과물인 여러 수식들은 컴퓨터의 발달로 인해 자동화가 많이 되었고, 로공입의 수식들 역시 마찬가지입니다. 그래서 로공입에선 식의 구체적인 계산은 어차피 컴퓨터가 할 터이니, 컴퓨터에게 어떻게 계산을 맡길지 시뮬레이션의 기반이 되는 알고리즘을 가르칩니다. 변화하는 기술개발과 시대 흐름에 맞추어, 4대 역학을 비롯한 다양한 과목들에도 컴퓨터가 할 수 있는 계산을 훈련하는 것이 아닌, 컴퓨터에게 그러한 계산을 시키는 법 등 다른 관점에서의 접근이 필요하다고 생각됩니다. 기계공학도를 꿈꾸는 학생들, 또 이미 진학한 학생들도 이와 같은 시각을 마음에 품고 접근하면 더 훌륭한 공학도로 성장할 수 있지 않을까 기대해봅니다.
고등학생분들이 기계과 강의에선 어떤 것들을 배우고, 또 어떠한 느낌으로 공부를 하는지 대략적인 감을 잡을 수 있도록 구체적으로 내용을 서술해 봤습니다. 제 서술 능력이 부족하고, 수학적으로 어려운 내용도 많아서 여러분이 얼마나 이해할 수 있을지는 잘 모르겠습니다. 혹시라도 궁금한 점이 있다면 얼마든지 댓글이나 제 개인 메일(cksdml1014@gmail.com)으로 문의주시면 되겠습니다. 또 로공입 교재 및 내용설명 영상은 modern robotics 홈페이지(http://hades.mech.northwestern.edu/index.php/Modern_Robotics)에서 확인할 수 있으니 관심 있는 분들은 살펴보셔도 좋을 것 같습니다.
많은 학생분들의 진로 고민 및 전공 결정에 조금이라도 도움이 되었길 바랍니다.
- 기계공학의 A to Z, 로공입의 기반 동역학을 포함한 4대역학이 궁금하다면? 전공백서: 4대역학 소개https://stementor.tistory.com/entry/%EA%B8%B0%EA%B3%84%EA%B3%B5%ED%95%99%EB%B6%80-4%EB%8C%80%EC%97%AD%ED%95%99-%EC%86%8C%EA%B0%9C
- 기계공학의 근본인 역학, 제조업의 기반기술 FEM이 궁금하다면? 전공백서: 역학과 설계https://stementor.tistory.com/entry/%EA%B8%B0%EA%B3%84%EA%B3%B5%ED%95%99%EB%B6%80-%EC%97%AD%ED%95%99%EA%B3%BC-%EC%84%A4%EA%B3%84
기계공학부: 역학과 설계
기계공학과를 졸업하여 취업하면 어떤 기술을 사용하게 될까요? 모든 제조산업에 쓰이지만 오직 기계공학과에서만 다루는 내용이 있다고요? 기계공학과의 근본, 역학과 설계를 소개해드립니다
stementor.tistory.com
기계공학부: 4대역학 소개
0. 전공백서: 4대역학 소개 안녕하세요! 공우 12.5기 기계항공공학부 송찬의입니다. 저희 기계공학과의 핵심이 되는 4대역학을 고등학생 분들이 이해할 수 있는 수준에서 소개해드리고자 합니다.
stementor.tistory.com

'전공백서 > 기계공학부' 카테고리의 다른 글
| 기계공학부: 응용유체역학 (0) | 2024.06.30 |
|---|---|
| 기계공학부: 역학과 설계 (6) | 2023.12.27 |
| 기계공학부: 인턴 연구 방법 및 경험 (1) | 2022.08.25 |
| 기계공학부: 창의공학설계 (1) | 2022.08.25 |
| 기계공학부 : 메카트로닉스 (565) | 2022.08.24 |





댓글