본문 바로가기

지난 연재물 - 수학 & 통계학89

08. Comparison with the Riemann Integral Comparison with the Riemann Integral 먼저 혼동을 막기 위해 Lebesgue measure \(m\)에 대하여 르벡 적분을 \[\int_{[a, b]} f \,d{m} = \int_{[a, b]} f \,d{x} = \int_a^b f \,d{x}\] 와 같이 표기하고, 리만 적분은 \[\mathcal{R}\int_a^b f\,d{x}\] 로 표기하겠습니다. 정리. \(a, b \in \mathbb{R}\) 에 대하여 \(a < b\) 이고 함수 \(f\)가 유계라고 하자. \(f \in \mathcal{R}[a, b]\) 이면 \(f \in \mathcal{L}^{1}[a, b]\) 이고 \(\displaystyle\int_a^b f\,d{x} = \mathcal{R}\in.. 2023. 6. 20.
07. Dominated Convergence Theorem Almost Everywhere 지난 글에서 measure가 0인 집합 위에서 적분하면 결과가 0이 됨을 확인했습니다. 적분 입장에서 보면 measure가 0인 곳에서의 적분은 의미가 없다고 생각할 수 있겠죠? 그러면 앞으로 그런걸 무시해도 된다고 하면 어떨까요? 정의. (Almost Everywhere) \(P = P(x)\) 가 어떤 성질이라 하자.1 만약 measure가 0인 집합 \(N\)이 존재하여 성질 \(P\)가 모든 \(x \in E \setminus N\) 에서 성립하면, \(P\)가 \(E\)의 거의 모든 점에서 성립한다고 한다. 표기법. 위를 편의상 ‘\(P\) \(\mu\)-a.e. (almost everywhere) on \(E\)’로 적겠습니다. 확률론과도 연관이 깊은 정리 하나.. 2023. 4. 7.
06. Convergence Theorems Convergence Theorems 르벡 적분 이론에서 굉장히 자주 사용되는 수렴 정리에 대해 다루겠습니다. 이 정리들을 사용하면 굉장히 유용한 결과를 쉽게 얻을 수 있습니다. 먼저 단조 수렴 정리(monotone convergence theorem, MCT)입니다. 이 정리에서는 \(f_n \geq 0\) 인 것이 매우 중요합니다. 정리. (단조 수렴 정리) \(f_n: X \rightarrow[0, \infty]\) 가 measurable이고 모든 \(x \in X\) 에 대하여 \(f_n(x) \leq f_{n+1}(x)\) 라 하자. \[\lim_{n\rightarrow\infty} f_n(x) = \sup_{n} f_n(x) = f(x)\] 로 두면, \[\int f \,d{\mu} = \li.. 2023. 3. 31.
05. Lebesgue Integration Lebesgue Integration 르벡 적분을 단계적으로 정의하려고 합니다. \(X = (X, \mathscr{F}, \mu)\) 라고 계속 가정합니다. \(\mathscr{F}\)는 \(\sigma\)-algebra on \(X\), \(\mu\)는 \(\mathscr{F}\)의 measure 입니다. \(E \in \mathscr{F}\) 일 때, 적분을 정의하기 위해 \[\mathscr{F}_E = \{A \cap E : A \in \mathscr{F}\}, \quad \mu_E = \mu|_{\mathscr{F}_E}\] 로 설정하고 \(\int = \int_E\) 로 두어 (\(X, \mathscr{F}_E, \mu_E\)) 위에서 적분을 정의할 수 있습니다. 그러나 굳이 이렇게 하지 않아도.. 2023. 3. 20.
04. Measurable Functions Measurable Functions Lebesgue integral을 공부하기 전 마지막 준비입니다. Lebesgue integral은 다음과 같이 표기합니다. \[\int_X f \,d{\mu}\] 표기를 보면 크게 3가지 요소가 있음을 확인할 수 있습니다. 바로 집합 \(X\), measure \(\mu\), 그리고 함수 \(f\)입니다. 집합과 measure는 다루었으니 마지막으로 함수에 관한 이야기를 조금 하면 Lebesgue integral을 정의할 수 있습니다! 이제부터 다루는 measurable function 관련 내용은 일반적인 measurable space \((X, \mathscr{F})\)에서 논의합니다. 여기서 \(\mathscr{F}\)는 당연히 \(\sigma\)-algebr.. 2023. 2. 13.
03. Remarks, Measure Spaces Remarks on Construction of Measure Construction of measure 증명에서 추가로 참고할 내용입니다. 명제. \(A\)가 열린집합이면 \(A \in \mathfrak{M}(\mu)\) 이다. 또한 \(A^C \in \mathfrak{M}(\mu)\) 이므로, \(F\)가 닫힌집합이면 \(F \in \mathfrak{M}(\mu)\) 이다. 증명. 중심이 \(x\in \mathbb{R}^p\) 이고 반지름이 \(r\)인 열린 box를 \(I(x, r)\)이라 두자. \(I(x, r)\)은 명백히 \(\mathfrak{M}_F(\mu)\)의 원소이다. 이제 \[A = \bigcup_{\substack{x \in \mathbb{Q}^p, \; r \in \mathbb{Q.. 2023. 2. 3.
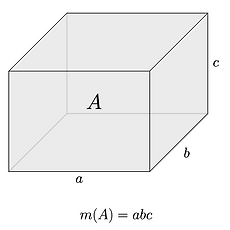
02. Construction of Measure Construction of Measure 이제 본격적으로 집합을 재보도록 하겠습니다. 우리가 잴 수 있는 집합들부터 시작합니다. \(\mathbb{R}^p\)에서 논의할 건데, 이제 여기서부터는 \(\mathbb{R}\)의 구간의 열림/닫힘을 모두 포괄하여 정의합니다. 즉, \(\mathbb{R}\)의 구간이라고 하면 \([a, b], (a, b), [a, b), (a, b]\) 네 가지 경우를 모두 포함합니다. 정의. (\(\mathbb{R}^p\)의 구간) \(a_i, b_i \in \mathbb{R}\), \(a_i \leq b_i\) 라 하자. \(I_i\)가 \(\mathbb{R}\)의 구간이라고 할 때, \(\mathbb{R}^p\)의 구간은 \[\prod_{i=1}^p I_i = I_1 \.. 2023. 1. 27.
01. Algebra of Sets Introduction 이 시리즈에서는 르벡 적분을 다룹니다. 르벡 적분 또한 함수의 그래프와 \(x\)축 사이의 ‘부호 있는 넓이’를 측정한다는 점에서 리만 적분과 유사합니다. 하지만 리만 적분에서는 \(x\)축을 잘게 잘라 넓이를 근사했기 때문에 적분 가능성이 함수의 연속성에 크게 의존하게 됩니다. 르벡 적분에서는 \(y\)축을 잘게 자름으로써 이러한 문제를 해결하고, 적분의 수렴정리와 같은 유용한 결과를 쉽게 얻을 수 있습니다. 참고사항 서울대학교 수리과학부 해석개론 및 연습 2 강의를 들으며 제가 정리한 강의 노트를 재구성했습니다. 강의 교재가 Principles of Mathematical Analysis (Walter Rudin)이기 때문에 이 책을 많이 참고하였습니다. 수학 용어 특성상 번역.. 2023. 1. 23.
집합의 기수와 무한집합 3 - 비가산집합의 예시, Power Set, Cantor Set Post 3 - 비가산집합의 예시, Power Set, Cantor Set 안녕하세요! 벌써 집합의 기수에 관한 마지막 포스팅이 되었습니다. 우리는 지금까지 (상당히 많은 사전 논의를 배제하고) 집합의 기수의 정의, 무한집합과 유한집합, 가산집합과 비가산집합에 대해 살펴보고, 비가산집합과 무한에 대한 연구를 촉발시켰던 칸토어의 정리를 살펴보았습니다. 칸토어 정리의 핵심은, 무한에도 '크기’가 존재하고, 모든 무한 집합의 '크기’가 같지는 않음을 보였음에 있는데요. 얼핏보면 자연수의 개수가 구간 [0,1][0,1][0,1]에 존재하는 실수의 개수보다 훨씬! 많아야 할 것 같습니다. 칸토어의 정리는 그 함의와 증명이 너무 반직관적이어서 당시 많은 수학자에게 비판을 받기도 하였다고 합니다. (와닿지 않으시더라.. 2021. 8. 20.

티스토리툴바