Vector Calculus 02. Power Series

멱급수

안녕하세요~ EsJay입니다. 어쩌다보니 글을 격주로 올리고 있네요. 저는 드디어 빅엿을 먹은 지옥의 기말고사 기간을 마치고 종강을 하였습니다!!(짝짝짝) 근데 다음주에 또 겨울학기 시작이네요.. ㅎㅎ 하. 뭐 어쩌겠습니까. 대학생의 본분대로 공부를.. 해야..죠.. ㅠㅠ

아니..왜..종강했는데..또 개강이야...

지난 번에 살펴본 수열과 급수의 기본적인 내용을 바탕으로, 오늘은 멱급수(power series)를 살펴보도록 할게요. 테일러 급수로 가는 3부작의 중간 단계로 출발합니다.

수열과 급수 ▶ 멱급수 ▶ 테일러 급수

일단 간단하게 멱급수의 정의와 개념을 한 번 살펴보고 들어가보실까요. 멱급수도 이름에 나와있다시피, 결국은 급수의 한 종류입니다. 직역하면 강한 급수...가 아니라 일반항에 지수(exponent)가 들어가 있는 형태이기 때문에 멱급수(power series)라고 부르지 않나 싶어요. 보통은 지수의 밑을 변수로 두는 함수의 꼴로 나타낸다고 합니다.

Definition 2.1. 멱급수(power series)

다음과 같이 주어진 실수 수열 $(a_n)$이 있다고 할 때, $$(a_n) = a_0 \:\:\: a_1 \:\:\: a_2 \:\:\: \cdots$$ 다음과 같은 $x$에 대한 무한 차수(infinite degree)의 다항함수 $\mathbf{a}(x)$를 $(a_n)$으로부터 얻어진 멱급수라고 한다. $$\mathbf{a}(x) \: := \: a_0 + a_1 x + a_2 x^2 + \cdots$$ 문자로서 다음과 같이 표기한다. $$\sum_{n=0}^{\infty} a_n x^n \:\:\: \mathrm{OR} \:\:\: \sum a_n x^n .$$

멱급수는 정의에서 보시다시피 다항함수(polynomial)입니다. 다항함수만큼 우리에게 익숙한 함수도 없겠죠. 무엇보다도 미분과 적분이 손으로 그냥 할 수 있을 만큼 간단하기 때문에, 이들에 대한 해석이나 그래프 작성은 그 어떤 함수들보다도 편리하게 할 수 있습니다. 그리고 이번 아티클의 후반부에서, 우리가 미적분학에서 자주 다루는 함수들(자연지수함수, 사인함수 등)이 놀랍게도 멱급수의 형태로 표현될 수 있음을 확인하게 될 거에요.

지수함수나 삼각함수가 다항함수로 표현될 수 있다니. 어떻게 그런게 가능하냐고요? 처음 보면 좀 믿기 어려울 수도 있겠지만 사실 앞으로 테일러 정리를 배우게 된다면 더욱 명료한 사실이 될 것입니다. 그리고 비단 지수함수나 삼각함수가 아니어도, 세상의 수많은 미분가능한 함수들이 이런 멱급수의 꼴로 치환될 수 있다는 것도 알 수 있게 될겁니다.

“ 멱급수의 수렴과 수렴반경

먼저 멱급수는 당연하겠지만 $x=0$에서 언제나 수렴합니다. 그 값은 수열의 첫 번째 항인 $a_0$이 되겠죠. $$\sum {a_n x^n} |_{x=0} \; = \; a_0$$ 그렇다면 다른 $x$값에 대해서 멱급수는 어떠한 수렴의 형태를 보일까요? 다음의 세 가지 예제를 살펴보면 답을 알 수 있습니다. 1장에서 배운 수렴판정법들을 한 번 써먹어 봅시다.

• Sample Problem 2.1.
  $\sum (n+1)^n x^n\;$은 오직 $x=0$의 한 점에서만 수렴함을 보이시오.

일반항판정법을 사용하면, $\;x \not= 0\;$일 때 $$\lim_{n→\infty} {(n+1)^n x^n} \not= 0$$ 임을 아므로 급수는 발산한다. □

• Sample Problem 2.2.
  $\sum x^n /n!$은 모든 실수 $x$에 대해서 수렴함을 보이시오.

급수의 형태에 $n!$이 있으므로, 비율판정법을 사용해보자. $$\left| \frac{x^{n+1}}{(n+1)!} \right/ \left. \frac{x^n}{n!} \right| \; = \; \frac{|x|}{n+1}$$ 이는 $\;n→\infty\;$일 때 $x$에 상관없이 0으로 수렴한다. 따라서 모든 $x$에 대해 이 급수는 수렴한다. □

• Sample Problem 2.3.
  $\sum x^n\;$은 $|x|<1$의 특정한 범위에서 수렴함을 보이시오.

$$\sum x^n = 1 + x + x^2 + \cdots = \lim_{n→\infty} \frac{1-x^n}{1-x}$$ $|x|>1$이면 분모가 발산하므로 멱급수는 발산한다. □

위의 세 가지 예시에서, 우리는 멱급수의 수렴과 발산에 대해서 오직 다음의 세 가지 케이스만이 존재함을 유추할 수 있죠.

• 오직 $x=0$에서만 $a_0$으로 수렴한다. (수렴 반경 0)
• 모든 실수 범위의 $x$에서 수렴한다. (수렴 반경 $\;\mathbf{\infty}$)
• $|x|<r$일 때 수렴하고, $|x|>r$일 때 발산하는 양의 실수 $r$을 갖는다. (수렴 반경 $\;\mathbf{r}$)

다만 세 번째 케이스의 경우, 수렴 반경의 두 경계점인 $x=r\;$과 $\;x=-r\;$에 대한 수렴·발산 여부는 멱급수에 따라 다를 수 있습니다. 이 두 지점에 대해 각각 수렴과 발산을 따로 파악해주어야 진정한 수렴 범위를 알 수 있습니다. 예를 들자면, $\sum x^n /n$은 수렴반경이 1인 멱급수인데 $x=1$일 때는 조화급수가 되어 발산하고, $x=-1$일 때는 수렴하는 교대급수가 되어 수렴하므로 수렴범위는 $-1\le x \lt1$이 될 것입니다.

멱급수의 형태가 다소 복잡하다면, 다음의 정리를 이용해서 멱급수의 수렴반경을 구할 수 있습니다.

Theorem 2.1. 멱급수의 수렴반경

멱급수 $\sum a_n x^n\;$에 대해, 만약 다음의 극한 $$\rho\;:=\;\lim_{n→\infty} \left| \frac{a_{n+1}}{a_n}\right|\;\;\in\;[0,\infty)$$ 이 존재한다면, 이 멱급수의 수렴반경은 $1/\rho$가 된다. 단, $\;\rho=0\;$인 경우는 수렴반경이 $\;\infty\;$인 경우이고, 극한이 ‘양의 무한대’로 발산하는 경우는 수렴반경이 0인 경우이다.

$$\frac{a_{n+1} x^{n+1}}{a_n x^n}\;=\;\frac{a_{n+1}}{a_n} x$$ 따라서 만약 $\;|x| < 1/ \rho\;$라면 비율판정법에 의하여 $$\lim_{n→\infty} \left| \frac{a_{n+1}}{a_n} x \right|\;=\;\rho |x| < 1$$ 이 되어 멱급수는 수렴함이 증명된다.
한 편, $\;|x| > 1/ \rho\;$라면 위와는 반대의 결과를 통해 멱급수는 발산하게 될 것이다. 따라서 증명이 완료되었다. □

멱급수의 수렴범위를 구하는 과정을 한 번 정리해볼까요. 첫째, Theorem 2.1.을 통해 멱급수의 수렴 반경을 계산한다. 둘째, 수렴 반경이 유한한 크기의 실수라면, 두 경계점에 대해서 따로 수렴과 발산을 판정하여준다. 셋째, 부등식의 형태로 수렴범위를 표기하여준다. 만약 수렴반경을 구하는 것만으로 충분하다면, 첫 단계만 진행하면 원하는 답을 얻을 수 있을 겁니다!

“ 멱급수의 기본정리

멱급수는 다항함수이긴 하지만, 특별한 점이 하나 있죠. 바로 차수가 무한하다는 점입니다. 우리가 지금까지 다뤄온 다항함수는 그 차수가 유한하였으며, 또한 그런 다항함수는 주어진 정의역(일반적으로는 실수 전체)에 대해 항상 미분과 적분이 간단하게 가능함을 알고 있습니다. 차수가 무한한 멱급수에 대해서도 성립할까요? 증명은 생략하겠지만, 아래의 정리는 멱급수도 기존의 공식과 큰 차이 없이 미적분이 가능함을 이야기해줍니다.

Theorem 2.2. 멱급수의 기본 정리

수렴반경이 $r(>0)$인 멱급수 $\;\sum_{n=0}^{\infty} a_n x^n\;$에 대하여,

• 멱급수 $\;\sum_{n=1}^{\infty} n a_n x^{n-1}\;$은 수렴 반경 $r$을 갖는다.
• 멱급수 $\;\sum_{n=0}^{\infty} \frac{a_n}{n+1} x^{n+1}\;$은 수렴 반경 $r$을 갖는다.
• $f(x):= \sum a_n x^{n}\;, \; x\in(-r,r)$으로 정의되는 함수 $f$에 대해 $$f'(x) = \sum_{n=1}^{\infty} n a_n x^{n-1}$$ $$\int_0^x f(t) dt = \sum_{n=0}^{\infty} \frac{a_n}{n+1} x^{n+1}$$

가 성립한다.

그러면 멱급수의 기본 정리를 이용해서, 몇 가지 급수가 실제로 어떤 값을 갖게 되는지를 살펴볼까요. 우리는 이미 $|x|<1$에 대해 $\sum x^n$이 1/(1-x)가 됨을 고등학교 때부터 알고 있습니다. 따라서 $(-1,1)$에서 정의되는 함수 $g(x)$를 $$g(x)\;:=\;\frac{1}{1-x}\;=\;\sum_{n=0}^{\infty} x^n$$ 으로 둔다면, $$g'(x) = \frac{1}{(1-x)^2} = \sum_{n=1}^{\infty} nx^{n-1}$$ 이 됩니다. 따라서 다음을 알 수 있겠군요. $$\frac{x}{(1-x)^2}\;=\;\sum_{n=1}^{\infty}nx^n$$ $x$의 정의역이 -1에서 1 사이임을 유의하면, $\;\sum_{n=1}^{\infty}\frac{n}{2^n} = 2\;,\;\sum_{n=1}^{\infty}\frac{n}{3^n} = \frac34$와 같은 결과를 얻어낼 수 있을 겁니다.

• Sample Problem 2.4.
  다음 급수 $\sum_{n=1}^{\infty}\frac{1}{n 2^n}$는 어떤 값을 가지는지 조사하시오.

앞서의 함수 g(x)를 그대로 사용하여 주면 $$\int_0^x{g(t)dt}\;=\;\int_0^x{\frac{1}{1-t}dt}\;=\;-\ln(1-x)$$ 이 되고, 멱급수의 기본 정리에 의해 또한 $$\int_0^x{g(t)dt}\;=\;\sum_{n=1}^{\infty} \frac {x^n}{n}$$ 이 된다. 따라서 $x$에 $1/2$를 대입하여 주면 $$\sum_{n=1}^{\infty} \frac {1}{n 2^n}\;=\;\ln 2$$ 가 된다. □

“ 멱급수 형태의 지수함수와 삼각함수

샘플 문제에서 무심하게 지나쳐온 급수가 하나 있습니다. 수렴반경은 $\infty$이고, 따라서 실수 전체에서 정의되는 다음의 멱급수를 $\mathrm{exp}(x)$라 정의하겠습니다 (이름부터 뭔가 지수함수의 냄새가 나는…읍읍) $$\mathrm{exp}(x):= \sum_{n=0}^{\infty}\frac{x^n}{n!}$$ 멱급수의 기본 정리로부터 이 함수는 다음과 같은 재미있는 성질을 갖는 것을 알게 됩니다. 심심하다면 직접 증명을! $$\mathrm{exp}'(x) = \mathrm{exp}(x)$$ 그런데 우리는 도함수가 자기 자신과 똑같은 함수를 하나 더 알고 있죠. 바로 자연상수를 밑으로 갖는 자연지수함수 $y=e^x$입니다. 직감적으로 알아채셨겠지만, 두 함수는 사실 동일합니다.

Theorem 2.3. 자연지수함수의 멱급수 표현

자연지수함수의 멱급수 표현은 다음과 같다. $$e^x=1 + x + \frac{x^2}{2!}+\frac{x^3}{3!}+\cdots = \sum_{n=0}^{\infty} \frac{x^n}{n!}$$

함수 $f\;\;:\;\;\Bbb{R}\;\;→\;\;\Bbb{R}$을 다음과 같이 정의하자. $$f(x)\;:=\;\mathrm{exp}(x)e^{-x}$$ $f$의 미분을 구하면, $$f'(x)=\mathrm{exp}'(x)e^{-x}+\mathrm{exp}(x)(e^{-x})'\\=\mathrm{exp}(x)e^{-x}-\mathrm{exp}(x)e^{-x}=0$$ 이 되어 $f$가 상수함수임이 밝혀졌다. 그런데 한 편 $f(0)=1\cdot1=1$이므로 $$f(x)=1\;\;→\;\;\mathrm{exp}(x)e^{-x}=1$$ 이 성립한다. 따라서 $\mathrm{exp}(x)=e^x$. □

자연지수함수의 멱급수 표현 중 앞의 일부항만 떼어낸 유한 차수의
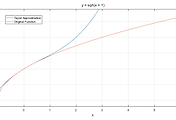
다항함수는 지수함수의 근사(approximation)에 쓰일 수 있습니다.
Source : http://calculus.seas.upenn.edu/

이번에는 조금 다른 모습의 두 멱급수를 소개해보죠. 둘 다 수렴반경은 역시 $\infty$이고, 따라서 실수 전체에서 정의됩니다. $$S(x)\;:=\;\sum_{n=0}^{\infty}(-1)^n \frac{x^{2n+1}}{(2n+1)!}\\ C(x)\;:=\;\sum_{n=0}^{\infty}(-1)^n \frac{x^{2n}}{(2n)!}$$ S랑 C를 보고 감을 잡으셨나요? 역시 멱급수의 기본 정리에 의해 다음을 압니다. $$S'(x) = C(x) \;\;\;,\;\;\; C'(x) = -S(x)$$ 그리고 우리는 또 서로간에 이런 관계를 가지는 두 함수를 알고 있죠. 바로 사인함수와 코사인함수입니다. 네, 그리고 이 함수쌍은 동일합니다.

Theorem 2.4. 사인함수, 코사인함수의 멱급수 표현

사인함수 및 코사인함수의 멱급수 표현은 다음과 같다. $$\mathrm{sin} x \;=\; x - \frac{x^3}{3!}+\cdots \;=\; \sum_{n=0}^{\infty}(-1)^n \frac{x^{2n+1}}{(2n+1)!}\\ \mathrm{cos} x \;=\; 1 - \frac{x^2}{2!}+\cdots \;=\; \sum_{n=0}^{\infty}(-1)^n \frac{x^{2n}}{(2n)!}$$

함수 $f\;\;:\;\;\Bbb{R}\;\;→\;\;\Bbb{R}$을 다음과 같이 정의하자. $$f(x)\;:=\;(\mathrm{sin}(x)-S(x))^2 + (\mathrm{cos}(x)-C(x))^2$$ $f$의 미분을 구하면, $$f'(x)=0$$ 이 되어 $f$가 상수함수임이 밝혀진다. 그런데 한 편 $f(0)=0^2+0^2=0$이므로 $$f(x)=0\;\;→\;\;(\mathrm{sin}(x)-S(x))^2 + (\mathrm{cos}(x)-C(x))^2 = 0$$ 이 성립한다. 따라서 $\mathrm{sin}(x)=S(x) \;,\; \mathrm{cos}(x)=C(x)$. □

사인함수 또한 멱급수 표현의 앞쪽 일부를 떼어서 근사에 사용할 수 있습니다.
Source : Dino57

위의 멱급수 표현에 대한 증명과정을 살펴보면, 다소 기술적인 부분이 들어가 있는 걸 확인하실 수 있을 겁니다. 사실 겉으로 보이는 증명 과정은 정말로 깔끔해 보이지만, 아마 저 증명을 처음 만든 수학자는 미분했을 때 0이 되는 함수의 형태를 고안하느라 머리 꽤나 썼을 거에요. 과연 다른 함수들은 이렇게 멱급수 표현이 가능할까요? 사인과 코사인, 그리고 지수함수의 경우에만 특별하게도 멱급수로 나타나는 건 아닐까요?

ㅎㅎ 왜 물어봤겠습니까. 정답은 '아니오'지요. 이제 다음 아티클에서는 3부작의 최종 목표가 될 테일러 급수(Taylor series)를 배우게 될 건데요, 바로 이 테일러 급수의 유일성과 존재성에 의해 수 많은 미분가능 함수들은 모두 멱급수로 표현 가능하다는 결론을 얻을 수 있습니다. 다음 아티클에서 만나뵙도록 할게요!