화학생물공학부: 분리공정

여기 아세톤 한 병이 있습니다.

우리에게는 매니큐어 지우개의 성분으로 꽤나 친숙한 물질인데요, 그럼에도 불구하고 가격을 보면 다소 사악하게 느껴집니다. 또 왜 불편하게시리 순도는 99.5%일까요? 깔끔하게 100%일수는 없는 것일까요?

저도 한때는 이렇게 생각했지만, 화학생물공학부의 분리공정을 수강하고 나서는 이것이 얼마나 뻔뻔한 생각이었는지 깨닫게 되었습니다.

저 99.5%의 아세톤이 시약장이 들어오기 전까지 어떤 과정을 거치는지 잠깐 볼까요?

출처: Tohaneanu, Madalina & Valentin, Plesu & Petrica, Iancu & Bumbac, Gheorghe & Ruiz, A.E. & Ruiz, J… (2014). Simulation and Process Integration of Clean Acetone Plant. Chemical Engineering Transactions. 39. 469-474. 10.3303/CET1439079.

예상 외로 굉장히 복잡하죠? 다시 보니 500mL에 7만원인게 기적일 정도입니다.

하지만 실질적으로 아세톤이 만들어지는 과정은 $C_3H_8O$의 isopropyl alcohol(IPA)에 열을 가하여 촉매의 도움으로 수소를 제거하는 반응과정이 전부입니다.

$CH_3CHOHCH_3→CH_3COCH_3+H_2$

나머지는 전부 잔여 반응물인 IPA로부터 반응 결과물인 아세톤을 분리해내는 증류, 흡수와 같은 분리과정입니다. 배보다 배꼽이 더 커보이는 상황이죠?

이처럼 어떤 물질을 얻기 위해서는 불순물을 제거하고 순도를 높이는 분리공정이 필수적이고, 그 중요성은 이루 말할 수 없습니다.

화학생물공학부의 분리공정 과목은 어떤 물질을 혼합물로부터 분리해내는 원리를 이해하고, 원리를 바탕으로 실제 공정을 설계해내는 방법을 가르칩니다.

구체적으로 어떤 내용을 배우는지 함께 알아봅시다.

1. 과목에서 배울 수 있는 내용

1) 분리공정의 종류

분리공정은 본질적으로 “혼합”이라는 자연적인 현상을 거스르는 과정입니다.

따라서 어떤 외부의 개입이나 장치를 투입해야 혼합물의 분리가 가능한데요, 무엇을 투입하냐에 따라 분리공정은 크게 네가지 종류로 구별됩니다.

. J. Henley; J. D. Seader; D. K. Roper, Separation Process Principles, 3rd ed., John Wiley & Sons, Inc, 2011.

(a) Phase Creation은 열과 같이 에너지를 투입해서 새로운 phase(상)을 형성하는 과정입니다. 대표적인 예시가 증류인데요, 액체 혼합물을 열로 가열하여 기체라는 새로운 상을 만듭니다. 이때 혼합물 중 휘발성이 높은 성분이 기체에 누적됨을 이용합니다.

(b) Phase Addition은 제3의 물질을 투입하는 방식으로 새로운 phase를 더하는 과정입니다. 예를 들어 액-액 추출의 경우 액체 혼합물에 새로운 액체 물질을 더하고 섞습니다. 이때 혼합물 중 새로운 액체 물질에 친화도가 높은 성분이 새로운 물질에 누적됨을 이용합니다.

© Separation by Barrier는 장벽을 이용하여 물질을 분리하는 과정입니다. 가령 기체 투과 (gas permeation)의 경우 막 경계로 혼합물 중 특정 기체분자만을 선택적으로 이동시킵니다. 특정 기체분자의 크기가 유독 작거나, 막에 대한 친화도가 높음을 이용합니다.

(d) Separation by an External Field or Gradient는 원심분리와 같이 외력을 가하거나 전기영동과 같이 전압 차이를 만드는 등의 방법으로 물질을 분리하는 과정입니다. 혼합물 성분들의 질량, 쌍극자 모멘트의 차이로 인해 외부 장에 대한 반응 정도가 다름을 이용합니다.

네 과정의 공통점은 전부 혼합물을 이루는 각 성분의 성질 차이를 이용한다는 점입니다. 물질마다 휘발성, 물질에 대한 친화도, 분자 크기, 질량, 쌍극자 모멘트 등 성질이 다르기 때문에 특정 조건에서 물질마다 서로 다른 거동을 보이고, 우리는 이를 잘 이용하여 분리 방법을 궁리해야 합니다.

그렇다면 혼합물의 분리 방법은 어떻게 선정할까요? 앞서 말했듯 일단 성분들의 성질 차이를 정확히 이해한 뒤 그것에 적합한 방법을 선택하면 됩니다. 예를 들어 도입부에 소개했던 IPA의 아세톤 혼합물을 분리해봅시다. 두 물질에 대한 정보는 다음과 같습니다.

물질	시성식	분자량	끓는점	녹는점	비중	용해도 (물)
Acetone	CH3COCH3	58.08	56.1oC	-95oC	0.784	miscible
Isopropanol	CH3CHOHCH3	60.10	82.3oC	-89.5oC	0.786	miscible

유독 차이나는 성질이 보이시나요? 분자량, 녹는점, 비중, 물에 대한 용해도가 모두 비슷하지만, 공교롭게도 끓는점의 큰 차이가 보입니다. 그렇다면 우리가 이용해야 할 분리공정은 명백히 증류겠지요?

증류에 대해 첨언하자면, 증류는 모든 분리공정 중에 가장 오래되고 기술적 성숙도가 높은 과정입니다. 비용과 효율 면에서 월등해서, 이용할 수 있는 특성 차이가 다양하더라도 증류가 가능하다면 웬만하면 증류를 이용하여 분리합니다. 물론 증류를 이용할 수 없는 혼합물도 있습니다. 불변끓는점혼합물(azeotrope)을 형성하거나, 효소와 같이 열에 약한 물질이 포함되어 있다면 증류 말고 다른 방법을 찾아봐야 합니다.

2) 분리공정의 원리

분리공정은 워낙 그 종류가 다양하기 때문에 각 공정마다의 이론과 원리의 묘사, 수학적 기술법이 상이합니다. 그럼에도 불구하고 모든 분리공정은 평형과 물질의 이동속도 두가지 관점으로 기술할 수 있습니다.

1) 평형의 관점

위의 왼쪽 그림처럼 상자에 A, B 두 물질이 균일하게 섞인 혼합물이 있습니다. 우리는 오른쪽 그림처럼 A, B가 각각 한쪽으로 농축되어 분리되길 원하고 있습니다. 두 상태의 본질적인 차이를 아시겠나요? 왼쪽은 물리화학적 성질과 조성이 동일한 상(phase)이 하나이고, 오른쪽은 성질과 조성이 상이한 두개의 상이 존재한다는 점입니다. 즉 분리공정에서의 “분리”는 곧 새로운 상을 만든다는 것과 동일한 이야기입니다. 물론 상자 안에 새로운 상이 거저 생기는 것은 아닙니다. Phase creation처럼 상자에 에너지를 가하거나, phase addition처럼 상자를 열어 제3의 물질을 넣어야 합니다.

그런데 어떻게 두개의 상이 동시에 존재할 수 있을까요? 그 이유는 두 상이 동일한 압력, 온도, chemical potential $μ_i=(∂G/∂n_ i)_{P, T,n'}$을 가지는 상평형 상태이기 때문입니다. 여기서 핵심은 상평형 상태에 놓인 두 상의 조성이 다르다는 점입니다. 다시 IPA와 아세톤의 예시로 돌아가봅시다. IPA와 아세톤의 액체 혼합물을 가열하여 기체상을 도입시키면 기체상의 조성에는 어떤 변화가 생길까요?

위의 IPA-아세톤 상평형 데이터에서 dew point curve는 기체상의 아세톤 몰분율, bubble point curve는 액체상의 아세톤 몰분율을 뜻합니다. 동일한 온도에서 두 curve가 가리키는 아세톤 조성을 보면, 상평형에 이른 기체상이 액체상보다 아세톤의 몰분율이 더 높음을 알 수 있습니다. 아세톤이 휘발성이 높기 때문에 직관적인 결과죠. 덕분에 액체 혼합물을 가열하여 얻은 기체 혼합물의 아세톤 순도가 높아졌습니다. 예를 들어 IPA와 아세톤을 1:1로 섞은 혼합물을 64^oC로 가열하면 아세톤의 몰분율이 0.75로 상승한 기체 혼합물을 조금 얻을 수 있습니다.

이처럼 상평형 조성은 새로운 상을 도입하면 얼마만큼의 분리를 이뤄낼 수 있는지를 보여주기 때문에, 분리공정 설계에 있어 상평형 조성을 정확히 알아내는 것이 매우 중요합니다. 상평형 조성은 실험을 통해서도 얻을 수 있지만 열역학 계산을 통해서도 얻을 수 있습니다. 바로 상평형에서 “chemical potential이 두 상에서 동일함”을 이용하는 것입니다. 수식적으로는 기체, 액체상 $G, L$에서 성분 $i$에 대해 $μ_{iG}=μ_{iL}$를 만족시키는 $x_i, y_i$를 찾으면 되는데요, 보통 $K_i=y_i/x_i$로 평형 조성비를 나타내는 평형 상수를 계산하게 됩니다.

열역학 계산을 통한 평형 상수 계산은 어떤 열역학 변수를 이용할지, 얼마만큼 이상 혼합물로 근사할지에 따라 방법이 다양한데요, 상황에 따라 근사한 간단한 식이 잘 맞기도 하지만 그렇지 않은 경우도 있기 때문에 적절한 계산법의 선정이 중요합니다. 설명하지는 않겠지만, 기체-액체 평형에 대해서는 다음과 같은 계산법이 있습니다.

- Raoult’s law:
$$K_i=\frac{P_{i}^{s}}{P}$$

- Modified Raoult’s law:
$$K_i=\frac{γ_{iL}P_i^s}{P}$$

- Rigorous formulation:
$$K_i=\frac{γ_{iL}P_i^s×\exp(\frac{(P-P_i^s)V_{iL}} {RT})} {P×\exp(\frac{B_{ii}(P-P_i^s)+Pδ_{ij}y_{22}}{RT})}$$

다시 상자 속 혼합물의 분리 문제로 돌아가봅시다. 해당 문제를 통해 설명한 “상평형을 통한 혼합물 분리” 원리는 실제 분리공정에도 적용되지만, 실제 분리공정은 두 가지 면에서 상자 속 상평형과 차이가 있습니다. 첫번째는 한번의 평형이 아닌, 여러 번의 평형을 이용한다는 점입니다. 몰분율 0.5의 IPA-아세톤 혼합물을 한번의 평형으로 높일 수 있는 몰분율은 최대 0.75가 전부이지만, 여러 번 평형 과정을 반복하면 순도를 더 높일 수 있습니다. 따라서 실제 분리공정은 처음 혼합물을 상자 속에서 평형이 이루어져 분리시키면, 상 하나를 꺼내서 다른 상자에 넣어 새로운 평형을 이루어 분리하기를 반복하는 과정입니다. 두번째 차이는 연속적인 흐름을 이용한다는 점입니다. 상자 안에 넣어 평형이 이루어질 때까지 기다렸다가 꺼내는 것이 아니라, 상자 안에 feed를 input으로 흘려주고, 평형이 이루어진 상들이 output으로 연속적으로 유출되게끔 합니다.

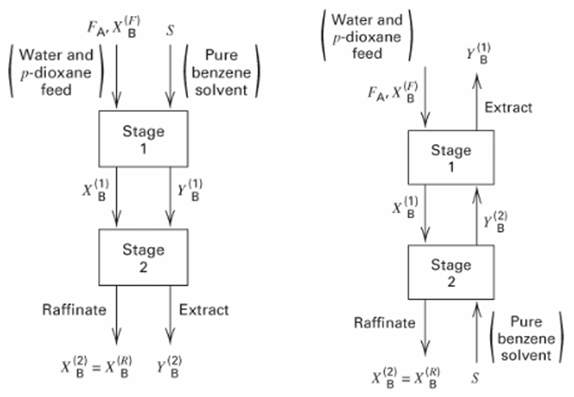
여러 번의 평형, 연속적인 흐름을 반영한 실제 분리공정과 비슷한 그림은 위와 같을 겁니다. 분리공정 중 액체-액체 추출을 나타낸 그림인데요, 구체적으로 물에 용질 p-dioxane이 용해된 액체 혼합물에 액체 benzene을 용매로 도입하여 benzene과의 친화도가 높은 p-dioxane을 추출하는 공정입니다. 물이 주성분인 상, 벤젠이 주성분인 상 두개 사이에서 p-dioxane의 평형이 이루어집니다. 보시다시피 흐름의 방향에 따라 왼쪽, 오른쪽 두가지 방식이 존재합니다. 두 상을 같은 방향으로 흘리는 왼쪽 방식을 Cocurrent cascade, 역방향으로 흘리는 오른쪽 방식을 Countercurrent cascade로 부릅니다.

그런데 두 방식으로 추출을 진행할 때 큰 차이가 있을까요? 한번 계산해 봅시다. Cocurrent cascade의 stage 1으로 들어오고 나가는 용질 (p-dioxane)의 mass balance를 세우고, 물, benzene 각각의 상에서 p-dioxane의 몰비율의 비인 평형 상수를 대입하면 추출되지 않고 빠져나오는 p-dioxane의 비율을 다음과 같이 나타낼 수 있습니다. (편의상 몰분율 x 대신 몰비율 X를 사용합니다. 평형 상수 또한 몰분율이 아닌 몰비율 기준으로 $K_{D'}=Y_B^{(E)}/X_B^{(R)}$로 나타냅니다.)

$X_B^{(F)}F_A=Y_B^{(E)}S+X_B^{(R)}F_A, Y_B^{(E)}=K_{D'}X_B^{(R)}$

$X_B^{(R)}=\frac{X_B^{(F)}F_A}{K_{D'}S+F_A}$

$\frac {X_B^{(R)}}{X_B^{(F)}}=\frac{1}{1+ε} ,ε=\frac{K_{D'}S}{F_A}$

결과적으로 $1/(1+ε)$ 만큼의 p-dioxane은 추출되지 않고 빠져나옵니다. 눈치채셨겠지만, 위의 계산은 한 개의 stage를 거친 계산과 다름이 없습니다. 생각해보면 stage 1에서 평형을 이룬 두 상이 다stage 2로 들어가도 아무런 변화도 생길 수가 없습니다. 즉 cocurrent cascade의 경우 stage를 몇 개를 거쳐도 stage 하나를 거친 것과 차이가 없어, 여러 개의 평형 단계를 거치는 것이 무의미한 방식입니다.

Countercurrent의 경우 stage 1과 stage 2에서 mass balance를 각각 세운 후 연립해야 추출되지 않는 p-dioxane 비율 계산이 가능합니다. 과정은 다음과 같습니다.

$$X_B^{(F)}F_A+Y_B^{(2)}S=Y_B^{(1)}S+X_B^{(1)}F_A, Y_B^{(1)}=K_{D'}X_B^{(1)}$$

$$X_B^{(1)}F_A=Y_B^{(2)}S+X_B^{(2)}F_A, Y_B^{(2)}=K_{D'}X_B^{(2)}$$

$$\frac {X_B^{(2)}}{X_B^{(F)}}=\frac{1}{1+ε+ε^2}$$

결과적으로 $\frac{1}{1+ε+ε^2}$ 만큼은 추출되지 않습니다. 확실히 한번의 평형보다는 더 많은 양을 추출할 수 있었는데요, cocurrent와 다르게 두 stage에 투입되는 조성이 서로 다르기 때문에 서로 다른 평형이 형성되어 stage 수를 늘리는 것이 유의미하였기 때문입니다. 귀납적으로, countercurrent cascade는 N개의 평형 단계를 설치하면 $\frac{1}{1+ε+…+ε^N}=\frac {ε-1}{ε^{N+1}-1}$만 남기고 전부 추출할 수 있습니다. 이러한 이유로, 대부분의 분리공정은 두 상을 역방향으로 흘리는 countercurrent cascade로 설계됩니다.

2) 물질전달속도의 관점

방금 함께 알아본 cascade를 보면서 조금 찝찝한 부분이 있지 않으셨나요? 사실 위의 설명에서 다소 억지스러운 가정이 있었는데요, 바로 각 stage에서 평형이 완전히 이루어졌음을 가정했다는 점입니다. 이론적으로 평형이 이루어지려면 무한대의 시간이 필요합니다. 연속적인 흐름으로 두 상을 흘려줄 때, 어떤 조성의 두 상이 만나는 시간은 찰나로 제한적이기 때문에 두 상이 평형조성에 도달하려고 하는 경향이 혼합물 분리의 구동력은 맞지만, 실질적인 분리 정도는 물질전달속도가 결정합니다. 예를 들어 IPA-아세톤 혼합물의 증류에서는 액체, 기체상에서 아세톤을 얼마나 빠르게 기체상으로, IPA를 얼마나 빠르게 액체상으로 이동시키느냐가 관건입니다. 물-p-dioxane-benzene 추출의 경우 p-dioxane을 얼마나 빠르게 물에서 benzene으로 이동시키느냐가 관건입니다.

그렇다면 어떻게 해야 물질전달속도를 빠르게 하여 분리 효율을 높일 수 있을까요? 두 상 사이의 물질전달 현상을 분석하여 힌트를 얻어봅시다.

두 상 사이의 물질전달은 상이 맞닿은 계면에서 일어납니다. 계면에서 두 상에서의 물질 조성이 평형 조성이 아니면 물질 이동이 일어나는데요, 두 상이 아주 찰나의 시간 동안에만 접촉하기 때문에 각 상의 조성으로부터 실질적으로 조성이 변화하는 구간은 위의 그림과 같이 계면과 아주 가까운 film에 불과합니다. 오랜 시간이 지나면 두 상의 모든 부분이 영향을 받아 평형 조성으로 변화하겠지만요. 따라서 물질전달은 각 상 film의 농도 기울기에 의해서 결정됩니다. 해당 방식으로 계면에서의 물질전달을 묘사하는 이론을 Two-film theory라고 합니다.

구체적으로 bulk에서의 농도를 $c_{Ab}$, 계면에서의 농도를 $c_{Ai}$, film의 두께와 확산계수를 $δ, D_{AB}$로 두면 물질전달의 flux는 Fick’s diffusion law에 의해 $N_A=\frac {(D_{AB})_G}{δ_G}(c_{Ab}-c_{Ai})_G=\frac {(D_{AB})_L}{δ_L}(c_{Ai}-c_{Ab})_G$로 표현됩니다. 이때 물질전달계수 $k=\frac {D_{AB}}{δ}$로 정의하고, 기체에 대해 농도 대신 분압으로 단위를 변환하면 $N_A=k_p(p_{Ab}-p_{Ai})=k_c(c_{Ai}-c_{Ab})$로 식을 바꿔 쓸 수 있습니다. 이때 계면에서 저항 없이 기체 측 분압과 액체 측 농도가 즉각적으로 평형조성을 이룬다고 가정하면, $c_{Ai}=H_Ap_{Ai}$가 성립합니다. 이를 flux에 대입하고 정리하면, 다음과 같은 식을 세울 수 있습니다.

$$N_A=\frac {p_{Ab}H_A-c_{Ab}}{\frac{H_A}{k_p}+\frac{1}{k_c}}=K_L(p_{Ab}H_A-c_{Ab}), \frac{1}{K_L}=\frac {H_A}{k_p}+\frac {1}{k_c}$$

위의 식이 유용한 이유는 더 이상 우리가 알지 못하는 계면의 농도가 아닌 알고 있는 두 상의 농도를 가지고 flux를 나타낼 수 있기 때문입니다. 식에 새로 도입한 $K_L$이라는 변수는 총괄물질전달계수로, 이것이 분리공정에서의 물질전달의 속도를 결정합니다. $\frac{1}{K_L}=\frac{H_A}{k_p}+\frac{1}{k_c}$로 정의되는데, $\frac{H_A}{k_p}$는 개념적으로 기체의 물질전달저항, $\frac{1}{k_c}$는 액체의 물질전달저항을 의미합니다. 각 상의 물질전달저항이 클수록 $K_L$은 감소하고 물질전달 속도는 감소합니다.

그렇다면 어떻게 하면 분리공정에서 물질전달 속도를 빠르게 할 수 있을까요? 답은 이미 나왔습니다. 바로 $K_L$을 높이거나 계면의 면적을 넓히면 됩니다. $K_L$을 높이려면 각 상의 물질전달저항 $\frac {H_A}{k_p}$와 $\frac{1}{k_c}$을 낮춰야 하고, 곧 각 상의 물질전달계수 $k_p$와 $k_c$를 증가시켜야 합니다. 물질전달계수 $k=\frac{D_{AB}}{δ}$로 정의되었던 것을 기억하시나요? 물질전달계수는 film의 두께 $δ$가 감소하면 증가합니다. Film의 두께는 일반적으로 유속이 빠르면 감소하는데요, 유속이 빠를수록 혼합이 촉진되어 film이 더 얇아지는 것으로 직관적으로 이해할 수 있습니다. 보통 액체는 $δL∝v^{-2/3}$, 액체는 $δG∝v^{-0.7}$의 관계를 가집니다. 이야기가 길어졌습니다만, 결국 “각 상의 유속을 빠르게 하여 $K_L$을 높일 수 있다”가 결론입니다. 물론, 유속을 너무 빠르게 하면 다른 문제가 생기지만요…

계면의 면적을 넓히는 것은 두 상을 한정된 공간 안에서 최대한 많이 접촉시킨다는 의미를 가집니다. 한가지 방법은 위의 그림과 같은 충전물을 이용하는 것인데요, 위의 구조들은 부피 당 표면적이 굉장히 넓기 때문에 두 상 중 하나를 분리 장치 내에 연속적으로 분포시키고, 다른 하나를 충전물을 통하여 분산시켜 표면에 젖게 하는 방법으로 계면의 면적을 어마어마하게 증가시킬 수 있습니다. 충전물에도 급이 있는데요, 오른쪽에 있는 규칙적인 충전물이 효율이나 여러 면에서 왼쪽의 불규칙 충전물보다 좋습니다. 다만 그만큼 가격이 매우 비싸서 산업에서는 효율이 조금 떨어지더라도 왼쪽의 불규칙 충전물을 이용하는 경우가 많다고 하네요 ^^;

그럼 평형의 관점과 마찬가지로 물질전달속도의 관점으로도 분리공정을 묘사해 봅시다. 이번에는 흡수공정에 묘사해볼 건데요, 흡수공정은 기체 혼합물에 액체를 새로운 상으로 도입하여 기체 성분 중 일부를 액체로 이동시켜 분리해내는 공정입니다. 대표적인 예시는 공기로부터 이산화탄소를 물로 흡수시키는 공정으로, carbon capture의 한가지 방법이기 때문에 최근 들어서 더욱 중요하게 생각되는 과정입니다.

여기 $l_T$ 길이, $A_T$ 단면적의 충전탑이 있습니다. 충전탑 하부에는 이산화탄소와 공기가 혼합된 기체를 몰유량 $V$만큼 투입하고 상부에는 물을 몰유량 $L$만큼 흘려보내 countercurrent 방식으로 이산화탄소를 물로 흡수하려고 합니다. 이때 그림에 보이는 dl 미소길이의 충전탑에서 시간당 얼마만큼의 이산화탄소가 이동할까요? 일단 우리는 $N_A=K_L(p_{Ab}H_A-c_{Ab})$ 식을 알고 있습니다. 해당 flux에 $dl$ 미소길이의 충전탑 안에서 허용되는 표면적을 곱하면 이산화탄소의 전달속도가 계산될 겁니다. 표면적을 간단히 표현하기 위해서 충전탑 내의 단위부피 당 허용되는 표면적을 $a$로 정의하면, $dl$ 미소길이의 충전탑 내의 표면적은 $a×A_{T}dl$로 표현할 수 있습니다. 즉, 액체로 이동하는 시간당 이산화탄소의 몰수는 $dN=aA_{T}dl×N_A=K_LaA_T(p_{Ab}H_A-c_{Ab})dl$입니다. 한편 액체로 이동하는 만큼 액체 속 이산화탄소의 몰수는 시간당 $dN=\frac {LM}{ρ}dc_{Ab}$만큼 증가하게 됩니다. 두 식을 연립하면, 다음과 같은 적분식을 얻게 됩니다.

$$\frac {LM}{ρ}dc_{Ab}=K_LaA_T(p_{Ab}H_A-c_{Ab})dl$$
$$\frac{LM}{ρ} \int _{c_{Ab, out}} ^{c_{Ab, in}} {\frac {1}{p_{Ab}H_A-c_{Ab}}dc_{Ab}}=K_LaA_T \int _{0} ^{l_T}dl$$

$$l_T=\frac {LM}{ρK_LaA_T} \int _{c_{Ab, out}} ^{c_{Ab, in}} \frac {1}{p_{Ab}H_A-c_{Ab}}dc_{Ab}$$

위의 식은 최종적으로 물로 회수하고 싶은 이산화탄소의 농도 $c_{Ab, out}$가 주어졌을 때, 충전탑 높이를 얼마나 높게 해야 하는지 계산할 수 있음을 보여줍니다. 재밌는 점은 해당 식에서 $K_{L}a$가 분모에 들어가 있는데요, $K_L$이 증가할수록, 계면의 면적이 증가하여 $a$가 증가할수록 요구되는 충전탑 높이 $l_T$가 감소한다는 것입니다. 전에 논의한 분리 효율을 높이기 위한 두가지 방법이 식에 고스란히 드러나 있음에 주목합시다!!

3) 분리공정의 설계

마지막으로, 여태 익힌 분리공정의 원리를 바탕으로 증류 과정을 묘사하고 설계해봅시다. 휘발성이 높은 물질인 light key와 낮은 물질인 heavy key의 혼합물을 가열하여 분리해내는 것이 목표입니다. 증류탑은 다음과 같은 구조를 가집니다.

총 $N$개의 평형단으로 이루어진 증류탑입니다. 증류탑 내부에 기체 상과 액체 상이 공존하여 서로 접촉하며 평형 조성에 도달하기 위한 물질전달이 일어나면서 분리가 이루어집니다. 액체 혼합물인 feed가 $f$번째 단으로 들어오면 아래로 하강하여 재비기(reboiler)로 들어가고, 가열로 인해 기화되어 기체상이 발생하여 위로 상승하기 시작합니다. 상승하는 기체는 하강하는 액체와 countercurrent하게 접촉하는데요, 이때 light key가 액체로부터 기체로 꾸준히 이동하여 기체로 농축됩니다. 따라서 증류탑 상부로 이동할수록 light key의 조성이 커지고, 하부로 이동할수록 heavy key의 조성이 커지게 됩니다. 가장 상부인 첫번째 단에서 light key가 주성분인 기체가 응축기(condenser)로 들어가서 전부 액체로 응축됩니다. 응축된 액체의 일부는 증류액(distillate)으로 얻고, 일부는 환류(reflux)로 액체 상태로 다시 증류탑으로 돌려보내 하강하는 액체를 만듭니다. 이러한 과정으로 증류탑 내에서 기체, 액체 혼합물이 상승, 하강하기를 반복하여 light key와 heavy key를 농축, 분리해내는 과정이 증류입니다. 어때요? 구조는 복잡해보였지만 분리공정의 원리를 토대로 설명하니 충분히 이해가 되지요? ^^

분리공정의 꽃은 설계입니다. 증류탑 운용 시 조절할 수 있는 변수들은 환류비, 증류탑의 온도와 압력, 공급물 유량, pressure drop, 응축기/재비기 형식, 탑 높이, 직경 등등 정말정말 다양합니다. 이러한 상황 속에서 증류탑에서 $x_D$의 light key 몰분율을 가지는 증류액을 얻기 위해서는 증류탑을 어떻게 설계해야 할지 안내하는 중요한 방법이 있는데요, 바로 McCabe-Thiele graphical method입니다.

McCabe-Thiele method는 물질 수지를 바탕으로 작성되는 operating line과 기체-액체 평형을 바탕으로 작성되는 equilibrium line을 이용하여 특정 단수의 증류탑 내 분리 현상을 묘사하는 작도법입니다. 모든 stage에 있어 액상의 몰유량이 $L$, 기상의 몰유량이 $V$로 일정한 상황을 가정합니다.

Feed stage 윗부분인 정류부(rectifying section)의 액상, 기상, 증류액 몰유량을 $L, V, D$로 표현하면 (a)와 같은 control volume에서 물질수지식을 다음과 같이 세울 수 있습니다.

Total mole balance:
$$D=V_{n+1}-L_n=V_n-L_{n-1}=\cdots =V_1-L_0=const>0$$

Component mole balance:
$$Dx_D=V_{n+1}y_{n+1}-L_nx_n=\cdots =V_1y_1-L_0x_0=const>0$$

Component mole balance를 정리하면 $y_{n+1}=\frac {L_n}{V_{n+1}}x_n+\frac{D}{V_{n+1}}x_D$이고, $L, V$가 일정한 상황이므로 증류탑 내의 액상, 기상 내 성분의 몰분율 간 관계는 $y=\frac{L}{V}x+\frac{D}{V}x_D$입니다. Total mole balance로부터 얻은 $V=L+D$로 $V$를 치환하고, $L/D$를 환류비(reflux ratio) $R$로 정의하면 정류부의 operating line 식이 유도됩니다.

$$y=\frac{R}{R+1}x+\frac{1}{R+1}x_D$$

Feed stage 아랫부분인 회수부(stripping section) 또한 마찬가지로 회수부의 액상, 기상, 농축물(bottoms) 몰유량을 $L, V, B$로 표현하고 (b)와 같은 control volume에 대해 $B=L- V=const>0, Bx_B=Lx_m- Vy_{m+1}=const>0$의 식을 세우면, 같은 과정으로 $y=\frac {L}{V}x-\frac{B}{V}x_B$ 식이 세워집니다. Bottoms에서의 환류비(boilup ratio)를 $V_B=\frac{V}{D}$로 정의하면 stripping section의 operating line 식이 유도됩니다.

$$y=\frac{V_{B}+1}{V_B}x-\frac{1}{V_B}x_B$$

Equilibrium line은 실험이나 앞서 설명한 열역학 계산을 통해 얻은 기체-액체 평형 데이터를 통해 도시됩니다. 두 operating line과 equilibrium line을 구했으면 McCabe-Thiele method를 사용할 준비가 되었습니다.

( c )를 보면서 이해해 봅시다. 시작은 $(x_D,x_D)$ 지점입니다. 우선 $y=x_D$를 그려 equilibrium line과의 교점을 찾습니다. 증류액은 $V_1$을 그대로 응축한 것이므로 $x_D=y_1$이고, 해당 교점의 $x$좌표는 $y_1$과 평형을 이루는 조성인 $x_1$이 됩니다. 이제 $x=x_1$을 그어 operating line과의 교점을 찾습니다. 이때 교점의 $y$좌표는 $x_1$와 동일한 구간을 지나는 기체의 조성 $y_2$가 됩니다. 해당 과정을 반복하면 가장 위의 stage부터 아래로 차근차근 하강하면서 모든 stage에서의 조성을 결정할 수 있습니다. 그림은 ( c )와 같이 계단식으로 그려질 것이고, 이를 stepping-off 과정이라고 부릅니다. 그리고 작도가 완료된 뒤, stepping-off를 반복한 횟수를 세면, $x_D$부터 feed의 조성 $z_F$, 농축액의 조성 $x_B$에 이르기까지 총 몇 개의 평형단이 존재해야 하는지 결정하게 됩니다.

짐작하셨겠지만, operating line이 어떻게 그려지냐에 따라 stepping-off 반복 횟수가 변화합니다. 예를 들어 환류비 R이 상승한다면 정류부 operating line $y=\frac{R}{R+1}x+\frac{1}{R+1}x_D$의 기울기가 1로 증가함에 따라 operating line과 equilibrium line의 간격이 더 넓어지고, 그만큼 stepping-off 시 계단이 크게 그려져 적은 stepping-off 횟수만으로도 작도가 종료됩니다. 극단적으로, $R→∞$인 왼쪽 그림의 경우 operating line은 $y=x$로, 이때 stepping-off의 횟수, 필요한 평형단의 개수는 최소가 됩니다. 위의 그림에서 비교해보면 환류비가 최대일 때의 평형단은 2개로, 적당한 환류비에서의 평형단인 5개보다 월등히 적습니다. 환류비가 클수록 평형단의 개수가 적어져 증류탑 높이를 낮게 설계해도 되겠지만, 그만큼 얻을 수 있는 시간당 증류액이 감소하기 때문에 trade-off가 존재합니다. 최적화가 필요하다는 것을 짐작할 수 있는 대목이죠.

사실 McCabe-Thiele method에 대해 feed의 종류나 feed stage에 따른 작도 방법 등 더 설명할 거리들이 있지만 분량상의 이유로 이만 줄이도록 하겠습니다…

2. 선배의 조언

화학생물공학부의 정체성은 무엇일까요? 워낙 다양한 주제를 다루기 때문에 단정하기는 어렵지만, 한가지를 뽑아야 한다면 대부분 가장 고전적인 화학공학의 주제인 “화학공정"을 뽑을 겁니다. 반응 중점의 화학과 생물을 빼면 남는, 물리화학적 원리를 기반으로 한 수식들로 가득찬, “화학생물"을 기대했던 저학년 친구들을 3, 4학년 들어 고통에 빠트리는 그 분야 말입니다.

저는 화생공의 공정과목들을 전부 수강하였는데요, 분리공정은 모든 과목들 중에 가장 다른 공정과목들과의 연계성이 짙은 과목이었습니다. 과목 설명을 보면서 느끼셨을텐데, 2학년의 물질 및 에너지 수지, 물리화학, 3학년의 유체역학, 화공열역학, 열 및 물질전달의 내용을 전부 사용해서 쌓아올리는 과목입니다. 그런 의미에서 저는 분리공정이 학부 화학공정의 끝판왕 격 과목이라고 생각합니다.

그렇기 때문에, 일단 화학공정에 관심이 있으시면 분리공정을 반드시 수강하세요. 그런데 저는 막상 바이오에만 관심이 있고 공정에는 딱히 뜻이 없는데도 홧김에 선택하였는데요, 덕분에 학기 중에는 상당히 후회했었습니다. 그런데 마친 후에 별개인 것처럼 느껴졌던 화생공의 과목들이 하나의 점으로 모여 정리되는 신기한 경험을 하고 나니, 후배님들께 추천을 안할 수가 없겠습니다. 이제 화학공학이 무엇인지 알 것 같은 느낌이랄까요? 화생공에 입학하여 학부 수준에서 화학공학을 뗐다고 당당하게 말하려면, 분리공정 들어야겠죠? ^^

분리공정을 수강하게 된다면 어떻게 공부해야 할까요? 사실 위에 언급한 다른 모든 과목들에 대한 이해가 탄탄하면 최소한의 공부만으로도 수강하는 데 무리가 없을 겁니다. 구멍이 존재한다면 복습의 시간이 필요하겠지만요. 저도 진도를 나갈 때마다 이전 과목 전공서들을 펼치는 횟수가 늘어가더군요. 수업을 마치고 어렵다, 이해가 되지 않는다는 느낌을 받으셨다면 분리공정 교재가 아닌 선수과목 교재를 펼치는게 더 도움이 될겁니다.

분리공정 과목만의 특징이 하나 있다면, McCabe-Thiele method와 같이 작도를 이용한 문제풀이가 많다는 점입니다. 작도가 간단한 편도 아니고요. 예를 들어 액체-액체 추출을 묘사하는 Hunter-Nash method의 경우 기본적으로 이성분계가 아닌 삼성분계를 다루기 때문에 삼각선도를 이용하여 작도를 하고, 상황에 따라 위와 같이 그림이 상당히 복잡해지기도 합니다. 그리고 수업시간에 배우는 단순화된 상황과 교재 연습문제에 등장하는 상황에는 굉장히 큰 간극이 있기 때문에 연습문제를 반드시 풀어보시길 바랍니다.

3. 진로 선택에 도움되는 점

모든 물질의 생산 과정은 혼합물로부터 물질을 분리하여 순도를 높이는 분리공정을 반드시 포함합니다. 어느 화학 공장에 가더라도 분리공정을 효율적으로 설계하는 것에 대한 수요가 항상 있다고 생각해도 됩니다. 사실 어떤 물질을 합성하는 과정보다 분리해내는 과정이 더 까다로운 경우가 많다고 합니다. 괜히 순도가 높은 물질이 비싼 것이 아니죠. 그렇기 때문에 어떻게 해야 적은 비용으로 최대의 분리를 이뤄낼 수 있을지에 대한 연구는 아주 중요한 주제입니다. 그만큼 돈이 많이 되기도 하고요. ^^

분리공정이 화학공정 쪽 직무/진로에 지대한 도움이 되는 과목은 맞지만, 냉정하게 말해서 모든 내용이 실용적인지는 잘 모르겠습니다. 특히 작도법의 경우, 과연 실무에서 작도법을 통하여 공정을 설계할까라는 의문이 듭니다. 실제로는 Aspen Hysys와 같은 process simulator를 이용할 테니 말입니다. 물론 작도법이 담고 있는 원리나 기반 지식은 정말정말 중요하지만 말이죠.

4. 맺음말

분리공정은 화학공정에 뜻이 있는 학부생들이 반드시 들어야 하고, 그렇지 않더라도 화생공의 화학공정 과목들을 총정리한다는 면에서 의미가 있어 추천하는 과목입니다. 여태까지 배운 지식들이 실제 공정을 설계하는 데 어떻게 사용되는지 체감하게 되는 과목이기도 하고요. 수업시간 교수님의 말씀을 인용하자면, 화학생물공학부에 들어왔으면 분리공정은 수강해야 하지 않을까요? ^^