안녕하세요, 공우 13.5기 화학생물공학부 윤성은입니다. 오늘은 화학생물공학부의 필수전공인 화학공정실험(공실)에 대해 소개해드리고자 합니다.
1. 강의 소개
1.1 강의 개요
화학생물공정실험(공실)은 화학생물공학부 필수전공으로 주로 3학년 2학기 또는 4학년 1학기에 수강합니다. 해당 강의는 화학공정과 관련된9가지 실험을 진행하며, 반응공학, 유체역학, 열 및 물질 전달부터 공정제어나 분리공정과 같은 강의의 내용을 포함합니다.
매주 실험을 진행하며, 실험 전에는 예비보고서를, 실험 후에는 결과보고서를 작성합니다. 각 보고서에는 추가 과제로 문제들이 포함되어 있으며, 예비보고서에는 미리 사용할 용액의 조성을 구해보거나 관련 응용 분야를 조사하는 문제부터 실험의 결과를 분석하는 데 필요한 공식을 유도하고 실험 결과의 경향성을 예측하는 문제가 있습니다. 결과 보고서에는 실험 중에 관측할 수 있는 현상의 원인을 분석하거나 관련 심화 이론을 조사하는 문제가 포함됩니다. 올해부터 실험 시간에는 교안을 바탕으로 퀴즈를 보게 되며, 예비보고서와 결과 보고서에는 각각 최대 5장과 10장의 분량제한이 생겼습니다. 마지막으로 각 조별로 실험을 하나씩 맡아 발표하고, 기말고사까지 봐야 하는 강의입니다.
1.2 실험 요약
공실에서는 아래와 같은 9가지의 실험을 진행합니다.
- 열전달 : 열전달에서는 대류와 복사의 복합 열전달에 대한 실험과 온도센서에서 복사에 의한 오류를 측정하는 실험을 진행합니다.
- 유체역학 : 유체역학에서는 벤츄리미터 실험으로 유량을 통해 베르누이 정리를 확인하고, 만곡부와 부속부를 통해 유체의 에너지 손실에 대해 탐구합니다.
- 반응공학 : 반응공학에서는 CSTR 시스템에서 반응속도 상수를 구하고, 아레니우스 식을 사용하여 활성화 에너지를 구하는 실험을 진행합니다.
- 상평형 : 상평형에서는 일정 압력 하에서 혼합물의 조성에 따른 시스템의 온도 변화로 평형 상태에서의 거동을 이해하는 실험을 합니다.
- 증류 : 증류에서는 회분식 증류탑을 사용하여 두 액체 혼합물의 분리 및 증류 공정에 영향을 주는 요소를 분석합니다.
- 추출 : 추출에서는 용질을 갖는 액체(carrier)와 섞이지 않는 액체(solvent)를 추출탑에서 접촉시켜 물질전달의 효율에 대해 연구합니다.
- 흡착공정 : 흡착공정에서는 흡착현상과 등온선, 파과곡선을 이해하고 이를 해석하여 흡착탑을 설계하고 운전하는 방법에 대해 배우게 됩니다.
- 흡수 : 흡수에서는 물을 용매로 공기와 이산화탄소 혼합물에서 이산화탄소를 흡수하는 충전탑을 운영하면서 물질수지에 대해 공부합니다.
- 공정제어 : 공정제어에서는 직렬연결된 coupled tank 시스템에서 탱크의 수위를 제어하는 PID 제어를 시행하면서 제어의 기본적인 원리와 구현방법을 익힐 수 있습니다.
1.3 실험 예시
위의 실험 중 공정제어 실험에 대해 간략하게 소개해 드리겠습니다.
a. 실험의 목표
공정제어는 화학공정에서 안전하고 효율적인 운전 및 생산을 위해 필요하며, 시스템에서 측정이 가능한 변수들을 원하는 값으로 조절하는 데 사용됩니다. 이 실험에서는 PID 제어기를 이용해 coupled tank 시스템에서 탱크의 수위를 제어하고, 그 결과를 분석해보게 됩니다.
b. 공정제어의 배경이론
b.1 동적 모델
공정제어를 이해하기 위해서는 먼저 동적 모델링에 대한 이해가 필요합니다. 동적 모델은 시간에 따른 시스템의 변화를 나타내는 모델로, 입출력 변수 간의 관계를 미분방정식으로 나타냅니다. 실험에서는 탱크의 동적 모델을 질량수지와 베르누이 원리를 이용해 아래 식과 같이 유도가 가능합니다.
AdLdt=kvV−a2gLA\frac{dL}{dt}=k_v V-a\sqrt{2gL}
이때, VV는 펌프의 전압, LL은 탱크의 수위, kvk_v는 변환 상수, aa는 탱크의 출구 단면적, AA는 탱크의 본체 단면적입니다. 이와 같은 비선형 방정식은 아래의 개요를 따라서 풀게 됩니다.

b.2 모델의 선형화
이렇게 얻은 모델은 테일러 전개를 이용해 선형화하여 고전제어의 다양한 선형기법을 사용하기 쉽도록 선형 모델을 얻습니다. 정상상태와 현재 상태의 편차로 아래와 같이 모델을 변형할 수 있습니다. 이때, δV=V−VS,δL=L−LS\delta V=V-V^S, \delta L=L-L^S이며, 정상 상태에 가까울수록 잘 성립합니다.
AdδLdt=kvδV−ag2LSδLA\frac{d\delta L}{dt}=k_v \delta V - a\sqrt{\frac{g}{2L^S}}\delta L
b.3 전달함수와 라플라스 변환
다음으로는 라플라스 변환을 이용해 전달함수를 정의함으로써 단순한 곱으로 input과 output의 관계를 표현할 수 있습니다. 라플라스 변환된 입력 U(s)U(s)와 출력 Y(s)Y(s)의 비율을 전달함수 G(s)G(s)로 정의하게 되면, 입의의 입력 u(t)u(t)에 대해 라플라스 변환을 적용하고, 전달함수와 역 라플라스 변환을 적용해 출력을 구할 수 있습니다. 아래와 같이 전달함수를 정의할 수 있습니다.[2]
Gp(s)=Y(s)U(s)=K∗τ∗s+1G_p(s)=\frac{Y(s)}{U(s)}=\frac{K^*}{\tau^* s+1}
(K∗=kvasLSg,τ∗=Aa2LSg)(K^*=\frac{k_v}{a}\sqrt{\frac{s L^S}{g}}, \tau^*=\frac{A}{a}\sqrt{\frac{2 L^S}{g}})
b.4 PID 제어
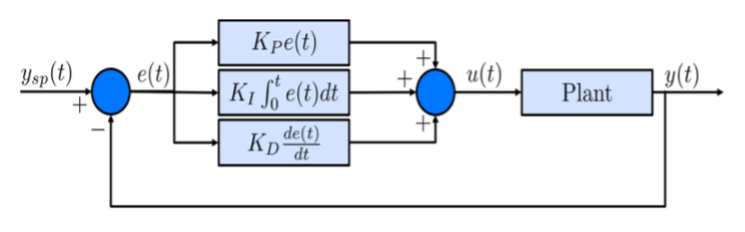
이번 실험에서 사용하는 PID 제어는 설정값과 출력의 오차 e(t)e(t)를 이용해 입력을 조절하는 제어 중 하나로, 오차, 오차의 적분, 오차의 미분값을 고려해 각 제어기의 gain을 조절합니다.[2]
- P (feedback) 제어는 에러에 proportional한 값으로 control합니다.
- I (integral action) 제어는 steady-state 에러를 없애는 방향으로 작동합니다.
- D (anticipation) 제어는 output의 빠른 변화를 억제해서 overshoot을 방지하고 안정성을 향상시킵니다.
아래의 그림과 같이 세 term의 합으로 input값을 컨트롤하게 됩니다.
b.5 블록 선도
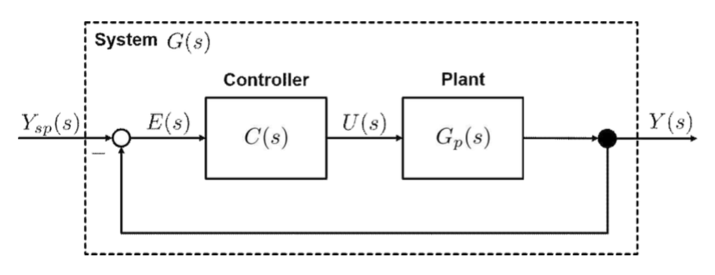
마지막으로 블록 선도를 통해 전체 시스템의 흐름을 시각화할 수 있습니다. 전체 시스템의 전달함수는 G(s)G(s), 제어기 전달함수를 C(s)C(s), 공정 전달함수는 Gp(s)G_p(s)로 정의하고 입력을 Ysp(s)Y_{sp}(s), 출력을 Y(s)Y(s)라 할 때, 전체 전달함수식을 나타낼 수 있습니다.[2]
G(s)=Y(s)Ysp(s)=C(s)Gp(s)1+C(s)Gp(s)G(s)=\frac{Y(s)}{Y_{sp}(s)}=\frac{C(s)G_p(s)}{1+C(s)G_p(s)}
c. 실험 방법
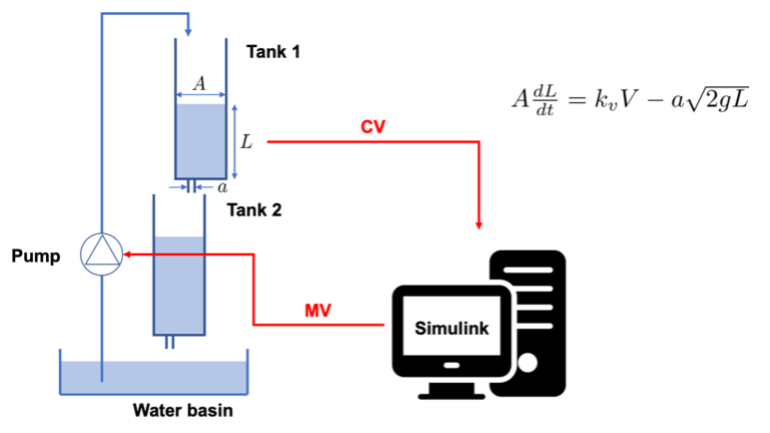
먼저 수조에 물을 넣고, Simulink에서 “Control” 파일을 실행해서 PID 제어기의 여러 변수들(Kp, Ki, Kd)을 바꿔가면서 결과를 관찰하게 됩니다. PID 제어기는 입력된 변수를 기반으로 측정된 수위와 설정 수위간의 오차를 이용해 펌프에 가할 전압을 결정하고, 그 전압은 아래에 위치한 water basin에서 상단의 탱크로 물을 끌어올립니다. 해당 실험은 공실에서 가장 빨리 끝나는 실험 중 하나라서 40-50분이면 끝낼 수 있습니다.
d. 결과 분석
PID 제어기의 파라미터를 바꿔가며 수위를 측정한 결과로 얻은 데이터를 그래프로 도시하면 아래와 같습니다.

d.1결과 분석
- P 제어에서는 set point 주변으로 빠르게 수렴을 하지만, offset이 나타나는 것을 관찰할 수 있습니다. 또한, 그래프가 진동하지 않고 잘 수렴하는 개형을 보이기 때문에 1차 제어임을 알 수 있습니다. 그래프의 개형으로부터 time constant와 같은 실험적 파라미터들을 계산할 수 있습니다.
- I와 PI 제어에서는 진동하는 그래프의 개형으로부터 2차 제어임을 확인할 수 있고, 그에 맞는 실험 파라미터를 계산할 수 있습니다.
- D 제어에서는 진동이 심하게 나타나고 잘 수렴하지 않는 경향성이 보이는데, 이는 오차의 미분값을 이용하는 제어이기 때문에 오차가 작아질수록 제어가 불안정해졌다고 볼 수 있습니다.
d.2 탱크와 PI 제어기의 전달함수 유도 및 분석
탱크와 PI 제어기를 전체 시스템으로 하는 블록 선도로부터 아래와 같은 전달함수를 유도할 수 있습니다.
G(s)=(Kp+KI/s)K∗τ∗s+11+(Kp+KI/s)K∗τ∗s+1=K∗(Kps+KI)τ∗s2+s+K∗(Kps+KI)G(s)=\frac{(K_p+K_I/s)\frac{K^*}{\tau^* s+1}}{1+(K_p+K_I/s)\frac{K^*}{\tau^*s+1}}=\frac{K^*(K_ps+K_I)}{\tau^*s^2+s+K^*(K_ps+K_I)}
- P 제어만을 사용하면 KIK_I가 0이고, 이로부터 이를 아래와 같은 식으로 나타낼 수 있습니다. 따라서 KpK_p가 증가함에 따라 K는 1에 근사되면서tau는 감소할 것이라고 예측할 수 있고, 실제로 실험에서도 유사한 경향성이 나타났습니다.
G(s)=Kτs+1,(K=K∗Kp1+K∗Kp,τ=τ∗1+K∗Kp)G(s) = \frac{K}{\tau s+1}, (K=\frac{K^*K_p}{1+K^*K_p}, \tau=\frac{\tau^*}{1+K^*K_p}) - I 제어만을 사용하면 KpK_p가 0이고, 이로부터 아래와 같은 식으로 나타낼 수 있습니다. 이때, K는 1이 되고 KIK_I가 증가함에 따라 τ\tau와 ξ\xi는 감소하며, 따라서 빠른 수렴이 나타날 수 있다고 볼 수 있습니다.
G(s)=Kτ2s2+2ξτs+1G(s)=\frac{K}{\tau^2s^2+2\xi \tau s+1}
(K=1,τ=τ∗K+KI′,ξ=12τ∗KKI)(K=1, \tau = \sqrt{\frac{\tau^*}{K+K_I'}}, \xi=\frac{1}{2\sqrt{\tau^*KK_I}})
d.3 실험 파라미터와 이론적 파라미터 차이 분석
위 그래프의 개형으로부터 얻은 실험적 파라미터와 이론적으로 계산한 모델 파라미터를 비교해서 선형화하는 과정에서 어떤 한계점이 있는지를 분석할 수 있습니다. 일반적으로, 비선형 미분방정식을 선형화하는 테일러 정리를 사용하게 되면, 운전점(정상상태)에서 벗어날수록 실제값과 차이가 많이 나타나게 됩니다. 실제로 실험에서도 실험에서 얻은 파라미터와 이론적인 파라미터의 오차율이 100% 이상이 나올 정도로 큰 것을 볼 수 있고, 정상상태에 가까운 상태에서 시스템을 운영해야 한다는 것을 알 수 있습니다.
d.4 각 제어방법의 문제점
- P 제어는 항상 set point와 차이가 나는 offset이 나타나는 한계가 있습니다.
- I 제어는 reset windup 현상이 나타나는데, set point가 변화할 때, 오차가 0이어도 적분값이 0이 아니게 되면서 제어가 멈추지 않게 됩니다.
- D 제어는 오차의 미분값을 사용해서 변수의 노이즈에 민감하고, 오차가 0에 가까워질수록 미분값의 차이가 커져 제어가 불안정하다는 한계가 있습니다.
d.5 PID 제어의 활용

위의 실험에서 사용한 PID 제어는 보다 복잡한 실제 공정에서도 활용이 가능합니다. 예를 들어 CSTR과 같은 시스템에서 유입할 유량을 조절해서 원하는 yield를 얻기 위해 control하는 문제에서도 적절한 파라미터 튜닝을 한 PID 제어기를 통해 product의 농도를 원하는 값으로 만들 수 있습니다.
나아가 TEP(Tennessee Eastman process)와 같이 실제 공장을 모사한 복잡한 시스템에서 여러 가지 measurable한 파라미터들을 control하는 데에도 PID 제어기를 활용할 수 있습니다. 이처럼 실제 현장에서 지금까지 이론적으로 배웠던 공학수학, 물질 및 에너지 수지, 반응공학, 공정제어와 같은 전공지식을 어떻게 활용할 수 있는지를 배울 수 있는 실험입니다.
2. 선배의 조언
공실은 로드가 많기도 하지만, 실험의 내용이 어려운 만큼 선수과목을 수강하고 듣는 것을 권장합니다. 전필로는 반응공학, 유체역학, 열 및 물질전달을 반드시 수강하시고, 전선으로 공정제어나 분리공정, 열역학을 들으면 더 도움이 될 것 같아요.
또한, 실험의 raw 데이터를 받았을 때, 어떻게 분석해야 할지 잘 모르겠다면 구글링을 통해 결과를 처리해주는 엑셀 파일을 찾아볼 수 있습니다. 잘 검색해보시고 그래도 모르는 점이 있다면 선배님들에게 도움을 요청하세요!
3. 맺음말
힘든 강의이지만, 공정실험을 기획하신 교수님의 열정과 애정을 많이 느낄 수 있었던 강의였습니다. 특히 교수님께서 각 조를 돌아다니시면서 실제 산업에서 어떤 방식으로 각 주제의 실험이 적용될 수 있는지를 자세히 설명해주셨던 것이 인상깊었습니다. 화생공 내의 분야가 다양하기 때문에 모든 학생들이 공정분야에 관심이 많기는 어렵지만, 화학공학에 있어서 다른 전공들과 다른 차별점이 되는 강의인 만큼 즐거운 마음으로 수강하시기를 응원합니다!
Reference
- 서울대학교 화학생물공학부. 화학생물공정실험, 공정제어, 서울대학교, 2024
- Seborg,DaleE.,DuncanA.Mellichamp,ThomasF.Edgar,andFrancisJ.DoyleIII.Process Dynamics and Control. Wiley, 2010
- Chen, Hong & Kremling, H & Allgöwer, Frank. (1995). Nonlinear Predictive Control of a Benchmark CSTR. Proceedings of the 3rd European Control Conference, Rome-Italy… 3247-3252.
- McAvoy, T. J., and Nan Ye. “Base control for the Tennessee Eastman problem.” Computers & Chemical Engineering 18.5 (1994): 383-413.

'전공백서 > 화학생물공학부' 카테고리의 다른 글
| 화학생물공학부: 기기분석 (1) | 2024.07.01 |
|---|---|
| 화학생물공학부: 물리화학 (1) | 2024.06.30 |
| 화학생물공학부: 분리공정 (0) | 2024.06.28 |
| 화학생물공학부: 세포생물공학 (0) | 2024.06.24 |
| 화학생물공학부: 유기화학 (0) | 2024.02.29 |





댓글