Vector Calculus 07. Vectors _ 02

벡터 _ 2편

앞서 1편에서 벡터(Vector)는 다음의 동등한 표현법으로 표시가 됨을 이야기했습니다.

1. $n$개의 실수(Real Number)로 이루어진 순서가 있는 리스트
2. $n$차원 공간 상에서 시점과 종점이 정해진 방향을 가진 선분

1편에서는 첫 번째 표현법을 이용하여 주로 벡터를 소개하였다면, 이번에는 두 번째 표현법을 이용해서 벡터를 요리해보도록 하죠. 사실 이번에 다룰 내용은 고등학교 기하와 벡터에서 다룬 내용들(평면벡터, 공간벡터)과 큰 차이는 없습니다만, 2~3차원 공간보다 더 높은 차원에서 벡터를 다루게 된다는 점이 차이라면 차이가 될 것입니다.

직선과 평면의 방정식

Definition 5.4. 평면(Plane)

$n$차원 카테시안 공간(cartesian space) $\Bbb{R}$ 에서, 하나의 일차방정식에 의해 구속되는 점들의 집합을 평면이라 한다. 즉, 어떤 평면 $P$는 다음과 같은 형태로 표현된다. $$ P:= \{ (x_1, \cdots, x_n)\in\Bbb{R}^n \;| \;a_1x_1+\cdots+a_nx_n=c\} \\ \text{단,}\;\; a_i\; (i=1,\cdots,n), \;c \text{는 실수} $$

$n$차원 공간에 존재하는 평면은 $(n-1)$차원을 가집니다¹. 또한 $\Bbb{R}^n$의 부분집합(subset)이 된다는 점도 자명하죠. 정의에서 알 수 있듯이, 평면을 특정하는 유니크한 요소는 바로 구속식(일차방정식)이기 때문에 우리는 자주 평면을 표현할 때 $$a_1x_1+a_2x_2\cdots+a_nx_n=c $$의 식만을 떼어내어 표시하곤 합니다. 이 식을 평면의 방정식(Equation of Plane)이라 부르겠습니다.

3차원 입체공간 상에서 표현되는 2차원 평면을 시각화한 그림

이러한 정의를 따랐을 때 다소 헷갈리는 점은 $n=2$일 때 발생합니다. 이 경우 평면의 방정식이 $$ \alpha x + \beta y = \gamma $$ 가 되는데, 우리는 이 식을 직선의 방정식이라 부르죠? 직선과 평면이 혼용되는 것인데, 이는 우리가 직선을 1차원과 동일시하여 생각하기 때문에 나타나는 상황입니다. 2차원 공간에서 Definition 5.4.에 의한 평면은 차원을 하나 낮춘 1차원이 되고, 곧 직선이 되는 것이죠. 2차원 공간 상의 평면은 1차원 직선이 된다는 사실을 확인해주시길 바랄게요.

Definition 5.5. 직선(Line)

$n$차원 카테시안 공간(cartesian space) $\Bbb{R}$ 에서, ‘해가 존재하는’ 서로 다른 $(n-1)$개의 일차방정식들에 의해 구속되는 점들의 집합을 직선이라 한다. 즉, 어떤 직선 $l$은 다음과 같은 형태로 표현된다. $$ l:= \{ (x_1, \cdots, x_n) \in \Bbb{R}^n \; | \; a_{i1}x_1 + \cdots + a_{in}x_n = c_i \;(i=1,\cdots,n-1) \} $$

공간의 차원에 상관없이, 직선은 항상 1차원을 가집니다. 직선의 방정식(Equation of Line)이라 불리는 $(n-1)$개의 일차연립방정식을 살펴보며 이야기해보도록 하죠. 우선 위의 연립방정식을 풀어 쓰면 다음과 같습니다.
$$ \begin{cases}
a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n = c_1 \quad \mathtt{(1)} \\
a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n = c_2 \\
\cdots \\
a_{(n-1)1}x_1+a_{(n-1)2}x_2+\cdots+a_{(n-1)n}x_n = c_{(n-1)}
\end{cases} $$ 해가 존재함이 전제되었으므로, $\mathtt{(1)}$식을 적절히 상수배하여 다른 식에 빼거나 더해주면, 다음의 결과를 얻습니다.
$$ \begin{cases}
b_{11}x_1+b_{12}x_2+\cdots+b_{1n}x_n = d_1 \quad \mathtt{(1)}\times \alpha \\
\color{white}{b_{21}x_1}+b_{22}x_2+\cdots+b_{2n}x_n = d_2 \quad \mathtt{(2)} \\
\cdots \\
\color{white}{b_{n1}x_1}+b_{(n-1)2}x_2+\cdots+b_{(n-1)n}x_n = d_{(n-1)}
\end{cases} $$ 즉, 두 번째 식부터 모두 $x_1$이 포함된 항이 사라졌습니다. 식이 $(n-1)$개 있으므로, 이러한 행위를 반복해줍시다. 세 번째 식부터 $x_2$가 사라지고, 네 번째 식부터 $x_3$이 사라지는 식으로요. 최종적으로 $\mathtt{(n-1)}$식은 오직 $x_{n-1}$과 $x_n$에 대한 식이 될 것입니다.
$$ ux_{n-1}+vx_n = w_{n-1} \quad \mathtt{(n-1)} $$ $\mathtt{(n-1)}$식에서 $x_{n-1}$은 $x_n$으로 표현되는 변수가 됩니다. 그리고 $\mathtt{(n-2)}$식을 생각해보면, 이 식은 $x_{n-2}$, $x_{n-1}$, $x_n$에 대한 식이므로, $x_{n-2}$ 또한 $x_n$에 대해 표현되는 변수가 됨을 알 수 있습니다. 거꾸로 반복하면, $x_1, \cdots , x_{n-1}$ 모두 하나의 독립변수 $x_n$에 대해 종속됨을 알 수 있죠. 즉, 직선은 하나의 독립변수에 의해 온전히 표현 가능하고, 따라서 언제나 1차원입니다².

직선과 평면의 벡터 표현법

평면의 벡터 표현

$n$차원 공간에서의 $(n-1)$차원 평면은 다음의 두 가지 요소에 의해 특정지어질 수 있습니다.

• 평면 위의 한 점(Point) $P$
• 평면의 법선(Normal) 벡터 $\mathbf{a}$

이제 $\Bbb{R}^n$ 상에서 점 $P$를 지나고, 벡터 $\mathbf{a}$에 수직한 평면의 방정식은 다음과 같이 기술됩니다.
$$ \mathbf{a}\cdot (X-P) = 0 $$ 여기서 $ X = (x_1,\cdots,x_n) $으로, 방정식의 미지수들이 됩니다. $ \mathbf{a} = (a_1,\cdots,a_n) $, 그리고 $ \mathbf{a}\cdot P = c $로 두면 위에서 보았던 평면의 방정식과 같아짐을 금방 확인할 수 있을 겁니다.

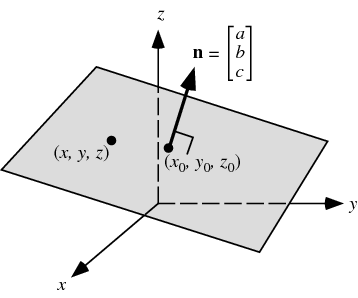
3차원 공간 상의 평면. 법선 벡터와 평면 상의 점이 표시되어 있습니다.

직선의 벡터 표현

$n$차원 공간에서의 1차원 직선은 다음의 두 가지 요소에 의해 특정지어질 수 있습니다.

• 직선 위의 한 점(Point) $P$
• 직선의 방향(Directional) 벡터 $\mathbf{v}$

이제 $\Bbb{R}^n$ 상에서 점 $P$를 지나고, 벡터 $\mathbf{v}$에 평행한 직선의 방정식은 다음과 같이 실수 범위의 매개변수 $t$에 의해 하나의 식으로 기술됩니다. $$ X = P + t \mathbf{v} $$ 여기서 $ X = (x_1,\cdots,x_n) $으로, 방정식의 미지수들이 됩니다. $ \mathbf{v} = (v_1,\cdots,v_n) $, $ P = (p_1,\cdots,p_n) $으로 두고, 매개변수 $t$를 소거하면 다음과 같이 $(n-1)$개의 연립방정식 형태로 표현되어, 위에서 보았던 직선의 방정식으로 표현됨을 확인할 수 있습니다.
$$ \frac{x_1 - p_1}{v_1} = \cdots = \frac{x_n - p_n}{v_n} \\ \text{(단,} \;\; v_i \neq 0 \text{인 경우)}$$

3차원 공간 상의 직선. 방향 벡터와 직선 상의 점이 표시되어 있습니다.

벡터의 선형결합, 선형독립

벡터를 이용한 기본도형의 표현법을 공부해보았습니다. 이보다 더 복잡한 형태의 도형(곡면, 곡선 등)의 표현은 나중에 다룰 수 있게 될 것입니다. 직선에서 잠깐 매개변수(Parameter)를 맛보기로 경험했는데, 이를 조금 더 복잡하게 사용하면 보다 복잡한 도형도 모두 표현할 수 있게 되죠.

벡터에 대한 포스트를 마치기 전에, 벡터를 다룬다면 절대 빠트려서는 안되는 개념을 하나 소개하고자 합니다.

Definition.5.6. 벡터의 선형결합(Linear Combination)과 선형독립(Linear Independence)

$\Bbb{R}^n$ 상에 주어진 $k$개의 벡터 $\mathbf{a_1},\cdots,\mathbf{a_k}$에 대하여,

Ⅰ. 임의의 실수 $t_1, \cdots, t_k$를 이용해 만들어지는 벡터 $ t_1\mathbf{a_1}+\cdots+t_k\mathbf{a_k} $ 를 $\mathbf{a_1},\cdots,\mathbf{a_k}$의 선형결합이라 한다.

Ⅱ. $\mathbf{a_1},\cdots,\mathbf{a_k}$ 중 적어도 어느 한 벡터 $\mathbf{a_i}$가 자기 자신을 제외한 다른 벡터 $\mathbf{a_1},\cdots,\mathbf{a_{i-1}},\mathbf{a_{i+1}},\cdots,\mathbf{a_k}$의 선형 결합으로 표현될 때, 즉 $$ \mathbf{a_{i-1}} = c_1\mathbf{a_1}+\cdots+c_{i-1}\mathbf{a_{i-1}}+c_{i+1}\mathbf{a_{i+1}}+\cdots+c_k\mathbf{a_k} $$ 이면 $\mathbf{a_1},\cdots,\mathbf{a_k}$는 선형종속이라 한다.

Ⅲ. $\mathbf{a_1},\cdots,\mathbf{a_k}$이 선형종속이 아닐 때, 즉 어떠한 벡터 $\mathbf{a_i}$도 자기 자신을 제외한 다른 벡터 $\mathbf{a_1},\cdots,\mathbf{a_{i-1}},\mathbf{a_{i+1}},\cdots,\mathbf{a_k}$의 선형 결합으로 표현되지 않을 때, $\mathbf{a_1},\cdots,\mathbf{a_k}$는 선형독립이라 한다.

벡터의 선형독립 정의에서 몇 가지 짚고 넘어갈 사항은, (1) 주어진 $k$개의 벡터 $\mathbf{a_1},\cdots,\mathbf{a_k}$가 별개의 벡터가 아니라, 일부는 동일한 벡터($\mathbf{a_i}=\mathbf{a_j}$)일 수도 있다는 사실과, (2) 선형결합 및 선형종속의 조건에서 실수곱에 곱하지는 실수들 $t$는 0이더라도 무관하다는 점입니다.

이러한 점을 생각했을 때, 선형독립(혹은 종속)과 관련된 다음의 주요한 특징을 확인할 수 있습니다.

• 영벡터(Zero vector)가 포함된 벡터 무리는 언제나 선형종속입니다.
• 평행하거나, 아예 동일한 두 벡터가 포함된 벡터 무리는 언제나 선형종속입니다.
• $\Bbb{R}^n$ 상의 축(Axis) 별 단위벡터 $(1,0,\cdots,0),\;(0,1,\cdots,0),\cdots,\;(0,0,\cdots,1)$ 들은 선형독립입니다.

임의의 벡터 집합이 주어졌을 때, 그들이 선형독립인지 아닌지 판별하는 방법이 있을까요? 아래의 정리는 단순 연립방정식의 풀이를 통하여 그 답을 알 수 있음을 알려줍니다.

Theorem 5.3. 선형독립 판별법

$\Bbb{R}^n$ 상에 주어진 $k$개의 벡터 $\mathbf{a_1},\cdots,\mathbf{a_k}$가 선형독립임은 다음과 동치이다:
아래의 방정식 $$ x_1 \mathbf{a_1} + \cdots + x_k \mathbf{a_k} = \mathbf{0}$$ 이 자명한 해 $(0,0,\cdots,0)$ 만을 가진다.

명제의 대우를 증명하자(선형종속 ↔ 자명하지 않은 해).

(←)
 방정식 $ x_1 \mathbf{a_1} + \cdots + x_k \mathbf{a_k} = \mathbf{0}$이 자명하지 않은 해 $ \mathbf{X} \neq \mathbf{0} $ 을 가진다고 하자. 0이 아닌 $x_i$값 하나를 고를 수 있으므로, 이를 가령 $x_1$이라 하자. 그러면 이제 벡터 $ \mathbf{a_1} $은 $$ \mathbf{a_1} = - \frac{x_2}{x_1} \mathbf{a_2}- \cdots - \frac{x_k}{x_1} \mathbf{a_k} $$이 된다. 선형종속의 정의에 의해, 이제 $\mathbf{a_1},\cdots,\mathbf{a_k}$는 선형종속임이 증명되었다. □

(→)
$\mathbf{a_1},\cdots,\mathbf{a_k}$이 선형종속이라 하자. 가령 $\mathbf{a_1}$이 다른 벡터들의 선형결합으로 표현된다고 하면, $$ \mathbf{a_1} = c_2 \mathbf{a_2}+ \cdots + c_k \mathbf{a_k} \\ \rightarrow -\mathbf{a_1} + c_2 \mathbf{a_2}+ \cdots + c_k \mathbf{a_k} = 0 $$ 이 되므로 방정식 $ x_1 \mathbf{a_1} + \cdots + x_k \mathbf{a_k} = \mathbf{0}$이 자명하지 않은 해 $(1, -c_1,\cdots, -c_k)$를 가짐이 확인된다. □

• Sample Problem 5.4.
  “$\Bbb{R}^3$ 상의 세 벡터 $(1,2,3),(2,3,4),(7,5,6)$의 선형종속 혹은 선형독립 여부를 판별하시오.”

Theorem 5.3.에 따라, 아래 연립방정식의 해를 살펴보는 것만으로 선형독립 여부를 따질 수 있다.
$$ \begin{cases}1x+2y+3z=0 \\2x+3y+4z=0 \\7x+5y+6z=0\end{cases} $$ 위에서부터 차례로 미지수를 소거하는 소거법을 사용하면,
$$ \begin{cases}1x+2y+3z=0 \\\color{white}{0x}-1y-2z=0 \\\color{white}{0x-0y}+3z=0\end{cases} $$ 이 된다. 아래 식부터 차례로 해를 구하면 그것은 $(0,0,0)$으로 유일하다!
따라서 벡터는 선형독립이다. □

벡터에 대한 설명은 여기에서 마무리됩니다! 아직 벡터 미적분학의 초반부이다 보니, 미적분보다는 벡터 위주로 설명이 되고 있습니다. 때문에 고등학교에서 배웠던 벡터에 관한 개념이 재기술되는 상황이 많았는데요, 다음 포스트부터는 일반적인 고등학교 수학에서 배우지 않은 개념이 속속 설명될 예정입니다 :) 

그 첫 번째 주자는 행렬(Matrix)입니다. 얼마 전만 해도 고등학교 교과과정에 꽤 높은 비중을 차지하고 있던 개념이었지만, 최근 그 종적을 감춘(...) 비운의 개념이기도 합니다. 행렬에 관한 설명과 함께, 선형 사상(Linear Mapping or Linear Transformation)에 대한 설명도 함께 곁들이기로 하죠. 다음 포스트에서 만나요!

---

1. 평면을 특정하기 위해 필요한 독립변수의 개수가 $(n-1)$개임을 뜻합니다. 예를 들어, $x_1,\cdots,x_{n-1}$만 설정된다면, $x_n$은 일차방정식에 의해 종속적으로 결정되겠죠? ↩

2. 이 논의는 다소 불완전합니다. 중간 계산과정에서 계수가 0이 되는 상황을 생각하지 않아서인데요, 이에 대한 자세한 논증은 벡터미적분학 부분에서는 중요한 파트가 아니니 생략하도록 하겠습니다. 자세히 알고 싶으신 분은 선형대수학의 가우스 소거법(Gaussian Elimination)을 검색해보세요. ↩