재료공학부: 재료결정결함
재료의 다양한 물성의 근간이 되는 결함을 종합적으로 다루는 재료공학부의 <재료결정결함> 수업을 소개합니다.
과목에서 배울 수 있는 내용
1. 흐름
<재료결정결함> 은 재료공학부의 4학년 전공 선택 과목입니다. 재료공학의 궁극적인 목적은 특정한 공학적 상황에서 재료의 performance를 향상시키기 위해 재료의 성질을 조절하는 것입니다. 한편 그 성질은 재료의 미세구조의 변화에 의해 민감하게 반응하며, 이때 그 변화는 바로 perfect crystal이라는 기준 구조에 **결함(defect)**이 도입되어 발생합니다. <재료결정결함>에서는 이 defect를 차원에 따라 3가지; 1차원인 선결함(line defect), 2차원인 면결함(plane defect), 그리고 0차원인 점결함(point defect) 으로 분류하여 살펴봅니다.
2. 선결함(line defect)
먼저 금속의 mechanical property를 설명하는 line defect인 전위(dislocation) 에 대해 배웁니다. 역학은 움직임이라는 결과를 힘이라는 원인을 가지고 설명하는 학문입니다. 힘을 줘도 변하지 않는 강체(rigid body)의 경우 모든 물체를 질량 중심을 기준으로 하나의 점입자(point particle)로 생각할 수 있는 반면, 일반적인 재료는 힘을 주면 변형이 일어나므로 역학을 기반으로 한 새로운 해석이 필요합니다. 일반적으로 변형(strain) 이라는 결과를 응력(stress) 이라는 원인을 가지고 설명하고, 이를 재료역학이라고 부릅니다. 한편 재료의 변형은 응력을 제거하면 다시 원래대로 돌아오는 탄성 변형(plastic deformation), 그리고 응력을 제거해도 원래대로 돌아오지 않는 소성 변형(plastic deformation) 의 2가지로 나뉩니다. 그 중 소성 변형이 일어날 때 재료의 미세구조의 변화를 바로 전위(dislocation)라는 개념을 가지고 설명합니다.
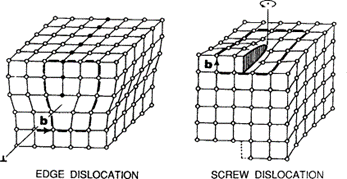
그림 1. 2가지 형태의 전위(dislocation)
소성변형은 재료 내부의 결합이 끊어져야만 가능한데, 결함이 없는 완벽한 재료에서 소성 변형이 일어나려면, slip이 일어나는 한 평면 위에 있는 모든 원자 간 결합이 끊어져야 하고, 이 메커니즘에 의하면 재료를 소성 변형시키기 위한 응력은 매우 커야 합니다. 그러나 실제로 재료를 소성 변형시키기 위해 필요한 응력은 이보다 훨씬 작습니다. 이를 설명하기 위한 방법이 재료 내 전위의 도입입니다. 재료 내부에 선요소(line element) 의 국소적인 이동이 있다고 가정했을 때 계산되는 응력은 훨씬 작아져 실제 값과 비슷하게 되는데, 이때 완벽한 결정 구조에 대해 국소적으로 이동한 선결함을 전위라고 부릅니다. 이 전위의 존재를 상정하면 외부 응력에 대한 재료의 반응(response), 나아가 재료 내부에 걸리는 응력장(stress field)까지도 계산할 수 있습니다. 전위라는 개념은 특히 철강을 활용한 구조재료 분야에서 중요한데요, 적절한 분포의 전위는 재료를 강하게 만들어주기 때문에, 전위가 아예 없는 재료를 만드는 것보다 오히려 적당한 밀도의 전위를 재료 내에 발생시켜 주는 것이 더 효과적입니다.
3. 면결함(plane defect)
재료 내부에는 선결함뿐만 아니라 결정면으로 이루어진 면결함도 존재합니다. 재료결정결함에서는 면결함중에서도, 입자의 쌓임 순서가 틀어져 생기는 쌍정(twin) 에 집중합니다. 쌍정은 2가지 매커니즘으로 생성될 수 있습니다. 앞서 설명한 전위가 slip 과정에서 결정의 한 쪽 끝에서 다른 끝으로 이동하면, slip 평면 위아래로 결정 내 원자 간격(atomic spacing)에 해당하는 만큼의 단차가 발생합니다. 이때 결정 내부의 결함은 더이상 선 형태의 결함이 아니라, 원자면 하나가 완전히 잘못 쌓인 것으로 해석할 수 있어요. 예를 들어, 구리, 은, 금, 알루미늄처럼 면심입방구조(Face-centered cubic structure) 를 갖는 결정에서는 결정면이 ABCABCABC… 순서로 쌓이게 되는데, 쌍정이 발생한다면 ABCABCBACBA…와 같은 쌓임 순서를 갖게될 수 있죠. 이렇게 전위의 움직임 때문에 발생한 쌍정을 Deformation twin이라고 합니다. 한편 결함은 반드시 그에 해당하는 에너지를 수반하게 되는데, 면결함의 경우 이를 stacking fault energy(SFE) 라고 합니다. 보통 결정의 크기에 따라 쌍정과 전위의 열역학적 평형 비율이 달라지게 되고, 이때 결정이 성장하면서 생기는 쌍정을 Annealing twin이라고 불러요. 결정의 크기가 커질수록 이 SFE의 비중이 커져서 결함이 쌍정 대신 전위로 많이 존재하는데, 반대로 나노-크기의 결정의 경우 전위보단 쌍정이 생기는 것이 에너지 측면에서 훨씬 유리합니다. 이때문에 거시적인 scale에서의 결정에서는 보기 힘든 5회 대칭 구조(five-fold symmetry)를 나타내기도 합니다. 혹은 쌍정에 의한 구조임을 강조하기 위해 penta-twinned structure라고도 불러요. 이 내용이 더 궁금하다면 stementor에 올린 "금지된 5회 대칭 구조" 게시물 을 참고해주세요!
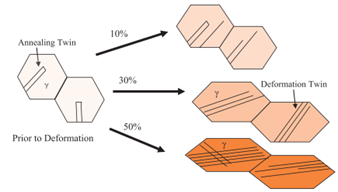
그림 2. 서로 다른 2종류의 쌍정의 형성 메커니즘1
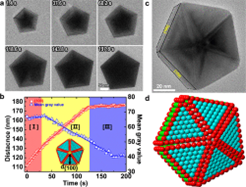
그림 3. nano-scale에서 나타나는 penta-twinned structure2
4. 점결함(point defect)
마지막 결함은 원자 하나에 해당하는 결함인 점결함이에요. 원자가 있어야 할 곳에 없으면 Vacancy, 있어야 할 원자가 없고 다른 원자가 있으면 Substitutional defect, 있으면 안되는 곳에 원자가 끼어있으면 Interstitial defect라고 부릅니다. Substitutional defect와 Interstitial defect의 경우 결정 내부에 강제로 impurity를 주입시켜 줄 때 발생할 수 있고, 결정 내부에서 이러한 결함의 거동은 열역학과 확산 법칙을 이용해서 설명할 수 있어요. 이 파트에서 전공필수과목인 재료열역학, 전공선택과목인 재료이동현상론에서 배운 내용들을 이용해 결정 내부에서 결함의 거동을 계산합니다. 한편, Vacancy는 열역학 법칙에 의해 impurity를 주입하지 않은 순수한 결정에서도 필연적으로 발생하게 됩니다. 좀 더 구체적으로 설명해보자면, 열역학 법칙을 이용해 계산해보면 재료 내에 필연적으로 존재할 수 밖에 없는 vacancy의 비율이 있고, 이 비율에 따라 재료 내부에는 결함이 반드시 존재해야 해요. 앞서 이야기했던 선결함(dislocation)과 면결함(grain boundary)이 결정 내 vacancy를 발생시키고 흡수하는 source와 sink로 기능할 수 있고, 심지어는 결정과 free surface 상의 경계도 vacancy를 발생시키는 source로 기능할 수 있어요. 이런 다양한 source를 통해 재료 내에 필연적으로 defect가 발생하게 됩니다.
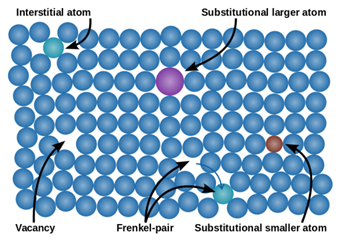
그림 4. 다양한 형태의 점결함3
점결함의 성질을 수식을 통해 보다 자세하게 이해해 보겠습니다. vacancy가 n개 존재할 때의 깁스 자유에너지는 로 쓸 수 있습니다. 먼저 은 vacancy formation energy에 해당하는 enthalpy 항입니다. vacancy의 생성과 소멸은 결합의 형성과 분해를 수반하므로, 이에 대응되는 엔탈피가 존재합니다. 한편 은 각각 vacancy의 비율에 따른 constitutional entropy(구성 엔트로피) 와 vibrational entropy(진동 엔트로피) 의 합으로 주어지는 엔트로피 항입니다. 완벽한 결정과 비교했을 때 vacancy가 생기게 되면 vacancy의 위치에 따른 각기 다른 microstate가 가능하기 때문에, 이에 의한 구성 엔트로피 가 생깁니다. 또한 vacancy가 생기면 결정 내부의 phonon mode가 변하게 되는데, 여기서 오는 진동 엔트로피 가 생깁니다. phonon mode에 관해서는 3학년 전공 필수 과목 <재료의 전자기적 성질> 에서 더 배울 수 있습니다. 결론적으로, 평형 조건 으로부터 vacancy의 평형 농도가 다음과 같이 얻어집니다.
식으로부터 온도가 T=0에 매우 가깝거나 vacancy formation energy가 무한에 가깝지 않으면, 평형 상태에서 vacancy는 필연적으로 발생한다는 것을 알 수 있습니다!
5. 멀티스케일 재료 전산모사(Multiscale materials simulation)
지금껏 살펴본 결함들은 그 크기가 매우 다양하고, 각각은 다양한 메커니즘을 통해 재료의 성질에 영향을 주게 됩니다. 특히 우리가 살펴보는 결함들은 대부분 수 개-수십 개 원자 단위 크기로 존재하는데, 우리가 원하는 재료의 물성은 대개 거시적인 스케일에서 나타나요. 재료의 물성에 관한 실험도 대부분 거시적인 스케일에서 이루어집니다. 반면 이러한 거시적인 물성의 원인인 결함에 대한 분석은 미시적인 스케일, 즉 옹스트롬(A) 단위에서 계산을 통해 이루어져야 해요. 계산 즉 시뮬레이션의 경우 스케일이 작을수록 쉽고 빨라집니다. 특히 원자 사이의 상호작용의 경우, 양자역학을 이용해서 매우 정확한 값을 구할 수 있어요. 대신에 공간적인 스케일이 작아지면 시간적인 스케일도 그에 비례해서 작아지기 때문에, 우리가 원자 단위에서 일어나는 일들을 알아내더라도 우리가 원하는 거시적인 스케일에서의 물성을 예측하기는 어려워요. 따라서 다양한 스케일에서 개별적인 방법론을 이용해 계산을 수행하고, 그 계산 결과를 연결시키는 멀티스케일 전산모사가 재료의 물성을 계산을 통해 예측하는 가장 효과적인 방법입니다. 먼저 양자역학에 기반을 둔 density functional theory(DFT) 를 통해 개별 원자의 양자역학적 성질과 전자기적 성질을 계산할 수 있어요. 그 다음 고전역학을 기반으로 원자 단위의 계산을 수행하는 molecular dynamics(MD) 를 통해 Atomic scale의 point defect를 분석할 수 있습니다. 그리고는 개별적인 전위의 거동과 상호작용을 계산하는 discrete dislocation dynamics(DDD) 를 통해 micro-scale의 line defect를 분석하고, 그 다음 Crystal plasticity Finite Element Model(CP-FEM) 을 통해 meso-scale의 surface defect를 분석할 수 있습니다. 최종적으로 재료를 하나의 연속체로 보아 물성을 계산하는 Continuum mechanics를 통해 재료의 물성을 거시적인 스케일에서 분석할 수 있어요.
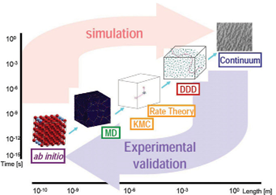
그림 5. 다양한 시공간 scale의 재료 물성 분석을 위한 toolbox4
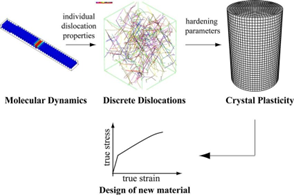
그림 6. 재료의 소성(plasticity) 예측을 위한 다양한 scale의 계산 방법론5
당시 재료결정결함 수업에서는 그 중에서 discrete dislocation dynamics simulation을 위한 패키지 중 MATLAB 기반의 dd3d (왼쪽)와 Linux 기반의 ParaDiS (오른쪽)를 이용하여 계산을 수행해, Frank-Read source 라고 불리는 전위의 형성 매커니즘을 직접 시뮬레이션 했습니다. 결론적으로는, 다양한 스케일에서 재료 내에 존재하는 결함의 종류와 거동을 이해하고, 이것이 재료 물성에 주는 영향을 이해하는 것이 본 과목의 목표라고 할 수 있어요.
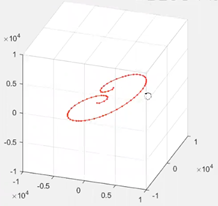
그림 7. MATLAB 기반의 dd3d 패키지를 이용한 Frank-Read source에서의 전위 형성 모사

그림 8. Linux 기반의 ParaDis 패키지를 이용한 Frank-Read source에서의 전위 형성 모사
선배의 조언
과목 특성 상 전공 필수 과목들의 내용의 단순 반복으로 느껴져 과목에 대한 흥미가 크게 떨어질 수 있습니다. 실제로 많은 내용이 재료공학부의 전공 필수 과목들에서 배우는 내용의 답습이기도 합니다. 제가 수강했던 2020년도 2학기 강의의 경우 교수님께서도 이 부분을 인지하고 계셨고, 전필 과목들에 해당하는 내용의 경우 직접 설명해주시기 보다는 수강생들에게 계속 질문을 던지며 논리 전개를 이어가셨습니다. 결론적으로 교수님께서 설정하셨던 당시 수업의 목표는 기존 전필 과목을 통해 이미 알고 있었다고 생각했던 내용들을 계속해서 새로운 관점에서 바라보는 것이었습니다. 수업 중 새로운 수식이나 이론을 접할 기회가 적지만, 역설적으로 기존에 배워서 알고 있는 내용이 많을수록 본 강의에서만 얻어갈 수 있는 insight도 많아집니다. 그렇기 때문에 전공 필수 과목들, 특히 결정학개론, 재료열역학, 재료의 기계적 거동은 전부 이수한 뒤 본 과목을 수강하는 것을 권장합니다. 수업은 교수님께서 다양한 서적을 참고하여 직접 제작하신 ppt로 진행되며, 수업 전후로 교수님께서 논문과 같은 Reading materials를 많이 추천해 주시기 때문에, 문제를 풀면서 공부하기보다는 논문들을 읽으면서 책상 앞에 백지를 펴놓고 우두커니 앉아 내가 아는 내용을 모두 써보면서 재료공학의 큰 흐름을 이해해 보는 것이 훨씬 도움이 많이 됩니다. (실제로 해당 수업 당시 교수님이 추천해주신 방법입니다!)
진로 선택에 도움되는 점
특정 분야에 국한하지 않고 재료 전반에서 나타나는 결함을 폭넓게 다루는 과목이다 보니, 특정 직종 혹은 특정 분야로 진출하기 위해 반드시 들어야 하는 느낌의 과목은 아닙니다. 다만 토론으로 진행되는 정말 몇 안 되는 재료공 전공 과목 중 하나이고, 과목 특성 상 수강생이 항상 적어 학생의 수업 참여도가 매우 높기 때문에 전공 면접 준비에 있어 크게 유리할 수 있습니다.
담당하시는 교수님의 전공이 금속재료냐, 세라믹 재료냐에 따라 강의의 중점 내용이 달라지기도 합니다. 가령 제가 들었을 당시에는 수업을 담당하셨던 최인석 교수님께서 금속 전공이셨기 때문에 금속 연구와 관련된 이야기를 많이 해주셨는데, 본 수업을 같이 수강했던 학부 동기가 대학원에 진학 후 High-entropy alloy에 관한 연구를 진행하는 데 있어 본 수업을 수강하며 쌓은 금속 내 결함에 관한 insight가 연구에 도움을 주고 있다고 털어놓기도 했습니다.
맺음말
완전히 새로운 내용을 배운다기 보다는, 지금까지 재료공학부에서 수강했던 많은 전공 과목들의 핵심 내용을 “결함”이라는 큰 틀에서 이해해보고자 하는 것이 본 과목의 목적입니다. 선결함-면결함-점결함이라는 정해진 커리큘럼이 있지만 그 안에서 무슨 자료와 reference를 가지고 어떤 방식의 수업을 할 것인지는 교수님들의 재량에 의해 결정되는, 상당히 자유로운 수업이었습니다. 사실 이 과목은 물리와 화학을 함께 전공하던 제가 재료공학을 이들의 단순한 열화(劣化)판으로 여기고 싫증을 느낄 무렵 수강한 과목입니다. 재료공학만의 originality는 어디에 있을지 고민하던 제가 이 과목을 수강하고 내린 결론은 “‘결함’의 관점에서 재료를 바라보고 사고할 수 있다”는 것이었습니다. 이 세상에 완벽한 “order”는 존재할 수 없으며, 재료, 나아가 자연현상이 다채로울 수 있는 이유는 “결함”이라는 것이 필연적으로 존재하기 때문입니다. 이것이 제가 재료공학을 전공하면서 배운 재료공학의 정수이자 철학입니다. 저와 비슷한 고민을 하고 있거나, “재료공학적 사고”가 무엇인지 궁금한 후배님들께 이 과목을 추천합니다.
N. Tewary, S. Ghosh, and S. Chatterjee, Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science 233, 763 (2017). ↩︎
B. Jin, M. L. Sushko, Z. Liu, X. Cao, C. Jin, and R. Tang, Journal of Physical Chemistry Letters 10, 1443 (2019). ↩︎
’Point defects in crystal structures’ By DaniFeri – Own work, (CC BY-SA 3.0) via Commons Wikimedia ↩︎
M. Samaras and M. Victoria, Materials Today 11, 54 (2008). ↩︎
S. Groh and H. M. Zbib, Journal of Engineering Materials and Technology 131, (2009). ↩︎

'전공백서 > 재료공학부' 카테고리의 다른 글
| 재료공학부: 반도체 집적 공정 (2) | 2023.08.28 |
|---|---|
| 재료공학부 : 재료이동현상론 (Transport Phenomena in Materials) (5) | 2023.08.28 |
| 재료공학부: 응용전기화학 (2) | 2023.07.10 |
| 재료공학부 : 고분자재료물리 (2) | 2023.03.17 |
| 재료공학부: 재료의 기계적 거동 (1) | 2022.12.20 |





댓글