예시로 알아보는 반응공학: 2번째, 전화율 & 반응기의 크기(2)
안녕하세요! 지난 시간에는 여러분들과 전화율의 개념과 반응기의 크기를 전화율을 사용하여 계산하는 과정을 공부해 보았습니다. 오늘은 지난 시간에 학습한 전화율을 사용해서 여러 반응기를 직렬로 연결한 반응에 대해 알아보고, 반응공학에서 중요한 개념인 공간시간과 공간속도에 대해 같이 알아보도록 하겠습니다!!
직렬 CSTR
오늘 게시물의 첫 부분에서는 CSTR과 PFR을 여러 개 직렬로 연결한 예시를 풀어보는 시간을 가지려고 합니다. 이를 해결하기 위한 첫 단계로 CSTR을 직렬로 연결한 경우에 대해 알아보도록 하겠습니다!
아래 그림은 두 개의 CSTR을 직렬로 연결한 모습입니다.

이때 반응을 전화율로 표현하기 위해서 각 단계의 전화율 Xi를 다음과 같이 정의하고 시작하겠습니다! Xi=i번째 반응기까지 반응된 양처음 들어간 양 두 반응기에 대해서 따로따로 설계방정식을 세운 다음, 전화율로 표시하면 이 문제를 해결할 수 있습니다. 반응기 1의 경우 다음과 같은 설계방정식으로 나타낼 수 있습니다. V1=FA0−FA1−rA 그 다음 반응기 2의 설계방정식을 마찬가지로 나타내면 다음과 같습니다. V2=FA1−FA2−rA 이 식을 정리해서 전화율로 나타내기 위해서는 각 지점의 몰 유량과 전화율 사이의 관계를 알아보아야 합니다. FA1과 FA2는 각각 다음과 같이 나타낼 수 있음을 전화율의 정의를 통해 알 수 있습니다. FA1=FA0(1−X1) FA2=FA0(1−X2) 이에 따라 두 반응기의 부피를 구하면 다음과 같이 계산된다는 사실을 간단히 확인할 수 있습니다. V1=FA0−rAX1 V2=FA0−rA(X2−X1) 식을 살펴보면 앞선 시간에 알아보았던 CSTR의 부피 식과 비슷하게, FA0−rA와 전화율을 곱한 형태의 식이 부피를 나타냄을 확인 가능합니다. 아래의 레벤스필 도표는 이러한 관계를 그래프로 나타낸 것입니다. 식으로부터 그래프의 모습이 연상되시나요?

직렬 PFR
다음으로는 PFR을 직렬로 연결했을 때에 대해서 알아보도록 하겠습니다! CSTR의 직렬 연결과 마찬가지로 PFR 2개를 연결한 경우를 통해서 PFR을 직렬 연결한 경우에 대해 같이 알아보겠습니다!
아래 그림은 두 개의 PFR을 직렬로 연결한 모습입니다.

이 경우도 CSTR과 마찬가지로 각 반응기에 대해서 따로따로 설계방정식을 세운 다음, 전화율로 표시해서 풀 수 있습니다. 우선 반응기 1의 경우와 반응기 2의 경우에 대해서 다음과 같은 설계방정식이 나타남을 지난 시간에 확인했습니다. V1=∫FA1FA01−rAdFAV2=∫FA2FA11−rAdFA 여기에 앞서 다룬 전화율의 식을 넣는다면, 두 부피는 다음과 같이 정리될 것 입니다. V1=∫X10FA0−rAdXV2=∫X2X1FA0−rAdX 어떠신가요? PFR의 전화율로 나타낸 설계방정식과 마찬가지로, 두 식은 각각 0과 X1, X1과 X2 사이에서 FA0−rA을 적분한 식임을 알 수 있습니다! 아래의 레벤스필 도표는 이러한 관계를 마찬가지로 그래프로 나타낸 것입니다. 식과 그래프를 동시에 확인하면서 식의 의미를 확인해보세요!

CSTR과 PFR을 한 번에 직렬로 연결하자
앞선 두 단락의 내용은 이전에 다룬 설계방정식을 단순히 반응의 처음부터 끝까지가 아닌, 적절한 전화율 사이에서 다루면 직렬 연결을 나타낼 수 있음을 이야기합니다. 그렇다면, 예시를 통해서 이러한 반응기의 직렬 연결에 대해 자세히 알아보도록 하겠습니다!
오늘 살펴볼 예시는 프로필렌으로부터 올레핀을 합성하는 Dimersol G 반응입니다. Dimersol G 반응의 경우, 올레핀 복분해 반응으로 노벨 화학상을 받은 프랑스 과학자 이브 쇼뱅이 제시한 반응입니다. 보다 자세하게 반응을 설명하면, 아래 그림과 같이 프로필렌의 dimerization 반응을 통해서 isohexene 이성질체들을 합성하는 반응입니다.

일반적으로, 이러한 Dimersol G 반응은 2개의 CSTR과, 1개의 PFR로 구성됩니다. 아래 사진에서 왼쪽에 있는 두 굴뚝이 CSTR, 그리고 오른쪽에 있는 라면처럼 꼬여 있는 파이프가 PFR입니다. 실제 반응은 앞의 CSTR에서 대부분 일어나게 되며, 뒤의 PFR은 반응물의 양을 충분히 줄이기 위해 마무리 반응을 하는 단계입니다.

이제, 이 반응을 수식과 레벤스필 도표를 통해 분석해보도록 하겠습니다. 분석을 보다 편하게 진행하기 위해서, 앞서 다루었던 레벤스필 도표의 FA0−rA vs X 곡선을 그대로 사용하겠습니다.

이 경우, 위 그림과 같이 레벤스필 도표를 그려낼 수 있습니다. 그렇다면 앞서 진행한 직렬 반응기의 분석과 마찬가지로, 수식을 통해서 위 도표를 분석하고, 각 반응기의 부피를 표현해 보겠습니다. 처음 2개의 반응기는 직렬 CSTR 연결과 동일하므로, 두 CSTR의 부피는 다음과 같이 됨을 쉽게 이해할 수 있습니다. V1=FA0−rA1X1 V2=FA0−rA2(X2−X1) 그렇다면, 마지막 PFR의 부피는 어떻게 될까요? X2에서 X3까지 반응이 일어나므로 결국 위 수식에서 적분 범위를 X2에서 X3까지 한 다음 식과 같이 나타나게 됩니다. V3=∫X3X2FA0−rAdX 즉, 반응기의 조합에 상관없이, 주어진 전화율 X1과 X2 사이에 CSTR이 있으면 직사각형으로, PFR이 있으면 적분 형태로 레벤스필 도표가 나타난다는 이야기로 정리할 수 있게 됩니다!
단열 조건일 때의 레벤스필 도표
지난 시간에 이런 이야기를 잠깐 다루고 넘어갔습니다. “즉, 온도가 일정하다면 FA0−rA은 전화율이 커질수록 커진다는 의미가 되겠네요! 그렇다면, 레벤스필 도표도 우상향하는 그래프가 됨을 알 수 있습니다.” 지금까지는 이렇듯 등온 가정 하에서 레벤스필 도표를 분석했습니다. 그렇다면, 다른 조건에서는 어떻게 될까요? 이런 의문을 가지고, 지금부터는 단열 조건일 때를 간단하게 짚고 넘어가도록 하겠습니다. 만일 발열 반응이 단열 조건에서 일어난다고 가정한다면, 반응이 진행됨에 따라 열이 발생되어 계 내부에 남아있게 됩니다. 즉, 온도가 상승하게 됨을 알 수 있습니다. 이에 따라, 반응물의 농도가 줄어듦에도 불구하고, 반응 속도가 오히려 증가할 수 있습니다. 그렇게 되면 FA0−rA은 감소하게 된다는 사실을 알 수 있습니다. 그렇게 되면, 그래프는 우하향하게 되고, 다음 그림과 같은 레벤스필 도표를 최종적으로 얻을 수 있습니다.
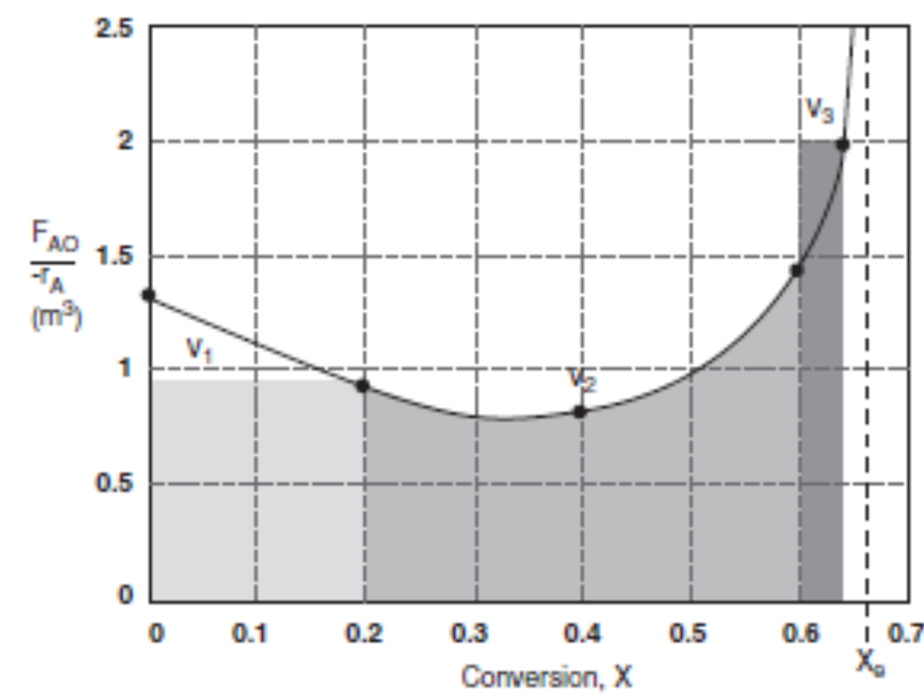
그렇다면, 하향하는 그래프에서는 CSTR과 PFR 중 어느 쪽이 유리할까요? 위 그림의 경우 전화율 0.3까지 함숫값이 감소함을 확인할 수 있습니다. 이때, CSTR을 사용하면 직사각형이므로 위 V1과 같은 형태로 부피가 나타나지만, PFR은 적분이므로 그래프 아래의 전체 넓이만큼 부피가 나타나게 됩니다. 즉 이번엔 반대로 PFR이 불리한 셈이 됩니다.
이제 예시를 통해서 이 경우의 반응기의 부피를 살펴보겠습니다. 지금 다룰 예시는 뷰테인의 이성질화 반응입니다. 뷰테인은 n-butane과 i-butane의 두 이성질체가 있습니다. 이 중 아이소뷰테인은 노말뷰테인으로부터 합성되며, 여러 화합물의 전구체로 사용되는 등, 다양한 용도를 가지게 됩니다.
이러한 뷰테인의 이성질화 반응은 다음과 같습니다. n−C4H10⇌i−C4H10 이 반응은 액상에서 단열 조건에서 일어나게 됩니다. 여기에 대한 데이터는 다음과 같이 알려져 있습니다.
| 변수 | data1 | data2 | data3 | data4 | data5 |
|---|---|---|---|---|---|
| X | 0.0 | 0.2 | 0.4 | 0.6 | 0.65 |
| −rA(kmol/m3⋅h) | 39 | 53 | 59 | 38 | 25 |
이에 따라, 이번 예시에서는 CSTR, PFR, 그리고 다시 CSTR을 사용하는 방식으로 아래 그림과 같은 직렬 반응기 연결을 가정하겠습니다.
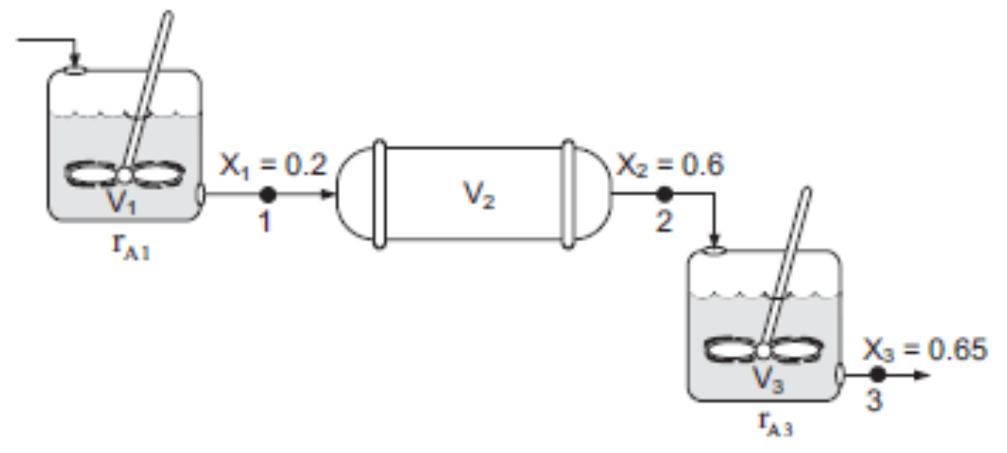
각 반응기가 얼마부터 얼마 사이의 전화율에서 사용되는 지가 표시되어 있으므로, 이제 이 데이터를 사용하여 레벤스필 도표를 얻을 수 있게 됩니다. 레벤스필 도표는 앞서 보았던 위의 그래프와 같게 나타나게 됩니다. CSTR과 PFR의 순서를 확인하실 수 있으신가요?
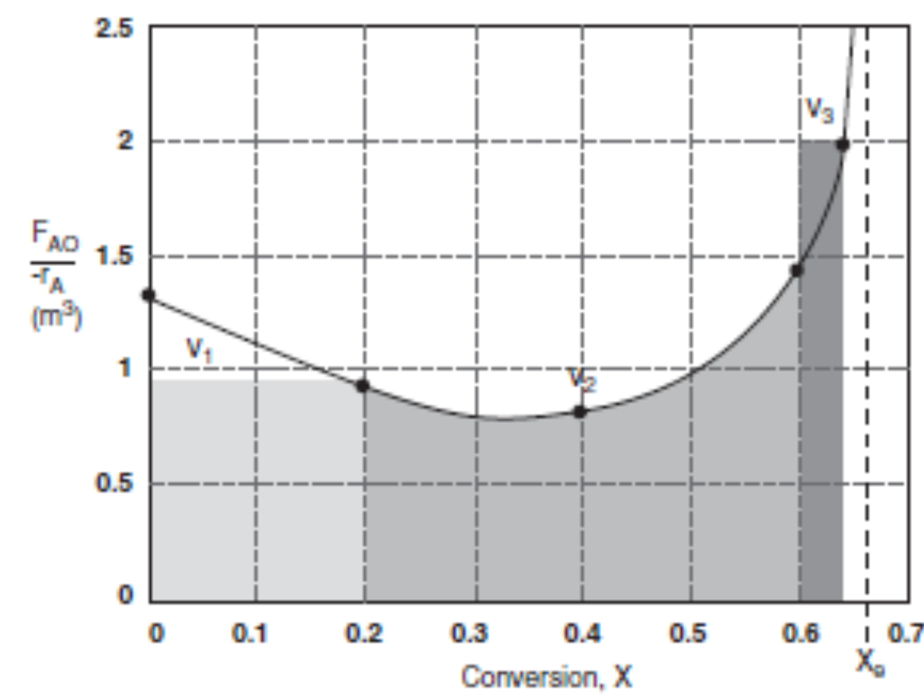
마찬가지로, 수식을 사용해서 부피를 계산해 보겠습니다. 먼저 첫 번째 CSTR은 V1=FA0−rAX1으로 됨을 앞선 직렬 CSTR의 분석으로부터 쉽게 파악할 수 있습니다. 그 다음, PFR은 첫 지점부터 끝 지점까지 그래프를 적분하여 부피를 얻을 수 있으므로 다음과 같이 부피가 나타남을 알 수 있습니다. V2=∫X2X1(FA0−rA)dX 마지막으로, 두 번째 CSTR의 경우 X2부터 X3 사이의 직사각형이므로 다음과 같이 부피가 나타나게 됩니다. V3=FA0−rA(X3−X2) 각각을 계산하면V1=188dm3, V2=380dm3, V3=100dm3로 나타남을 알 수 있습니다. 이처럼, 등온 조건이 아닌 다른 상황에서는 다른 형태로 레벤스필 도표가 나타남을 알 수 있습니다. 이 연재에서는 우선 간단한 경우인 우상향하는 그래프, 즉 등온 조건을 먼저 보도록 하겠습니다!
공간시간과 공간속도
끝으로, 반응공학에 있어 중요한 두 변수, 공간시간과 공간속도를 알아보도록 하겠습니다. 먼저 공간시간은 다음과 같이 정의됩니다. τ=Vv0 여기서 v0는 반응기로 들어가는 부피 유량입니다. 이 값은 전체 부피를 부피 유량으로 나눈 값이므로, 간단히 이야기해서 반응물이 반응기 안에 머무르는 시간이라고 생각할 수 있습니다.
그 다음 공간부피는 다음과 같이 공간시간의 역수로 정의됩니다. SV=v0V=1τ 이 값은 단위 시간 당 얼마나 많은 반응기의 부피 대비 얼마나 많은 양이 반응하는지를 의미합니다. 이때, 유량의 계산 방법에 따라서 공간속도를 다양하게 정의할 수 있게 됩니다.
첫 번째는 액체공간속도 LHSV입니다. 이는 액상 반응 혹은 액체-고체 촉매 반응에서 사용되는 값입니다. 이 경우 주어지는 액상 반응물의 유량을 섭씨 16~24도 가량에서 측정하게 됩니다.
두 번째로는 기체공간속도 GHSV 역시 있습니다. LHSV와 비교하면 어떤 의미인지 알 수 있으신가요? 이 경우는 기상 반응에서 사용됩니다. 이때 측정 조건은 흔히 STP라고 잘 알고 있는, 273.15K 및 1bar입니다.
이외에도, 고체 촉매 반응에서 사용되는 WHSV, 질량공간속도 역시 있습니다. 이 값은 지난번에 봤던 PBR과 같은 상황에서 사용되는 값으로, 부피 유량 대신 촉매의 질량으로 w0W와 같이 정의됩니다.
이러한 공간시간과 공간속도는 앞으로 다양한 반응기 상황을 다루면서 수식을 명료하게 정리하고, 이해하기 위해 많이 사용될 예정입니다. 정의를 잘 기억해주시면 감사하겠습니다!
용어 정리
오늘은 여러분들과 함께 반응기의 직렬 연결 및 공간시간과 공간속도에 대해 알아보았습니다. 어려운 부분이 있거나 궁금한 부분, 제안 사항이 있다면 답글로 남겨주세요!!
오늘 사용한 용어는 아래 표를 참고해 주시면 감사하겠습니다.
<사용 용어 표>
| 한국어 명칭 | 영어 명칭 |
|---|---|
| 직렬 연결 반응기 | reactors in series |
| 등온 | isothermal |
| 단열 | adiabatic |
| 공간시간 | space time |
| 공간속도 | space velocity |
| 부피 유량 | volumetric flow rate |
'지난 연재물 - 화학생물공학 > [반응공학] 예시로 알아보는 반응공학' 카테고리의 다른 글
| 예시로 알아보는 반응공학: 3번째, 반응 속도와 화학양론 (2) | 2022.08.01 |
|---|---|
| 예시로 알아보는 반응공학: 2번째, 전화율 & 반응기의 크기 (1) (1) | 2021.12.19 |
| 예시로 알아보는 반응공학: 1번째, 몰 수지(2) (1) | 2021.12.02 |
| 예시로 알아보는 반응공학: 1번째, 몰 수지(1) (1) | 2021.11.17 |
| 예시로 알아보는 반응공학 - 화학 공장에서는 무슨 일이? (1) | 2021.11.11 |





댓글