예시로 알아보는 반응공학: 1번째, 몰 수지(1)
안녕하세요! 오늘은 여러분들과 반응공학의 첫 장, 몰 수지(mole balance)를 같이 알아보려고 합니다. 먼저 지난 시간에 간단하게 짚고 넘어간 내용을 되짚어 보면서 시작해볼까 해요! 지난 시간에 하수처리장의 예시를 여러분들과 이야기하면서 반응기의 설계에 있어서 중요한 요소를 몇 가지 다루고 넘어갔습니다. 바로 반응 속도식, 투입하는 물질의 양, 그리고 반응기의 모양입니다. 오늘은 이런 요소들을 조절해서 수치적으로 반응기의 설계를 어떻게 할 수 있는지 알아볼 계획입니다.
반응 속도
첫 번째로 반응기에서 빠질 수 없는 부분인 반응의 속도식을 짚고 넘어가 보려고 해요! 이 글을 보고 계신 분들 중 일반화학이나 물리화학을 공부하신 분들은 반응 속도에 대해서도 공부하신 분이 많을 것이라고 생각합니다. 첫 날 목차에도 나타낸 만큼 반응 속도는 뒷 부분에서 자세히 다루고, 여기서는 복습 차원에서 정의 정도만 간단하게 공부하도록 해요.
예시로 $aA + bB \to rR + sS$의 반응을 생각해 보겠습니다. 반응물 A의 반응 속도를 나타내고 싶을 때, 반응공학에서는 이를 다음과 같이 나타냅니다. $$-r_A =- \frac {1}{V} \frac {dN_A}{dt} = \frac{(A의 \space 감소량)}{(부피) \times (시간)}$$ 즉, 단위 부피 & 시간 당 몰 수의 변화량을 반응 속도라고 정리할 수 있겠네요. 그런데 왜 $r_A$ 앞에 마이너스 기호가 붙을까요? 바로 A는 시간이 지날수록 양이 감소하는 반응물이기 때문입니다. 이 반응에서는 a몰의 A와 b몰의 B가 사라지면 r몰의 R과 s몰의 S가 생겨날 텐데요, 이를 수식으로 나타내면 $\frac{-r_A}{a} = \frac{-r_B}{b} = \frac{r_R}{r} = \frac{r_S}{s}$와 같이 계산할 수 있습니다. 이처럼 생성물의 반응 속도에는 마이너스가 붙지 않는 것을 확인할 수 있습니다. 각각의 반응 속도는 실험을 통해서 농도와 관련이 있음을 알고 있는데요, 이 부분은 다음에 다뤄 보도록 해요!
일반적인 몰 수지식
이제 본격적으로 몰 수지식에 대해서 알아보도록 합시다! 반응기에서 앞에서 다룬 반응이 일어날 때 반응물 A의 변화를 간단하게 아래와 같은 모습으로 생각해 봅시다.
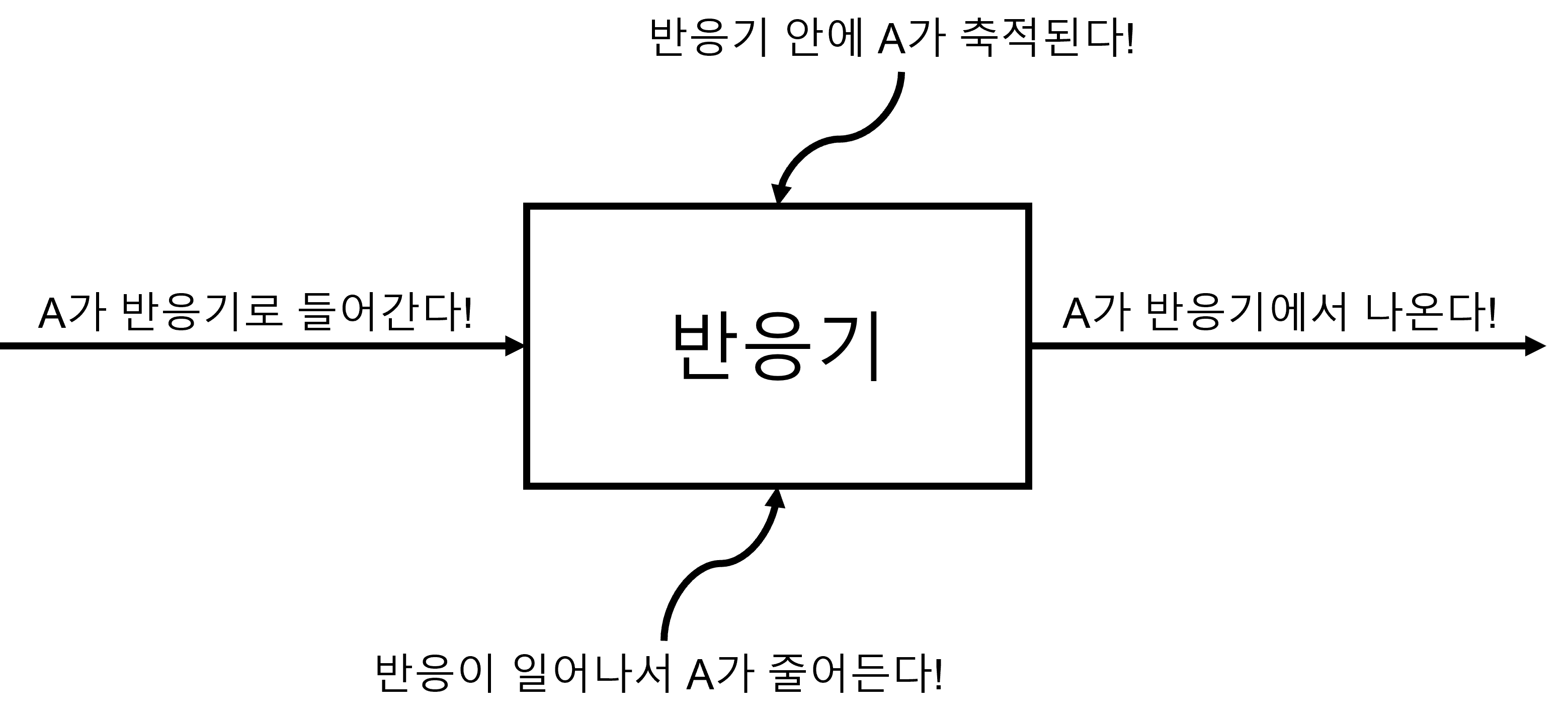
그림에 나온 것처럼 A는 반응기로 들어가거나, 반응기에서 나오고, 반응을 통해 생성/소모됩니다. 그리고 들어가는 A의 양에서 나오는 A와 소모되는 A의 양을 빼면 남아서 축적되는 A 역시 있다는 점을 확인할 수 있습니다. 이걸 수식으로 정리해보면 다음과 같습니다. $$\mathrm{In}-\mathrm{Out}+\mathrm{Generation}=\mathrm{Accumulation}$$ 아래 그림처럼 각 항목의 A의 양을 나타내면 다음과 같이 일반적인 몰 수지식을 얻을 수 있습니다.
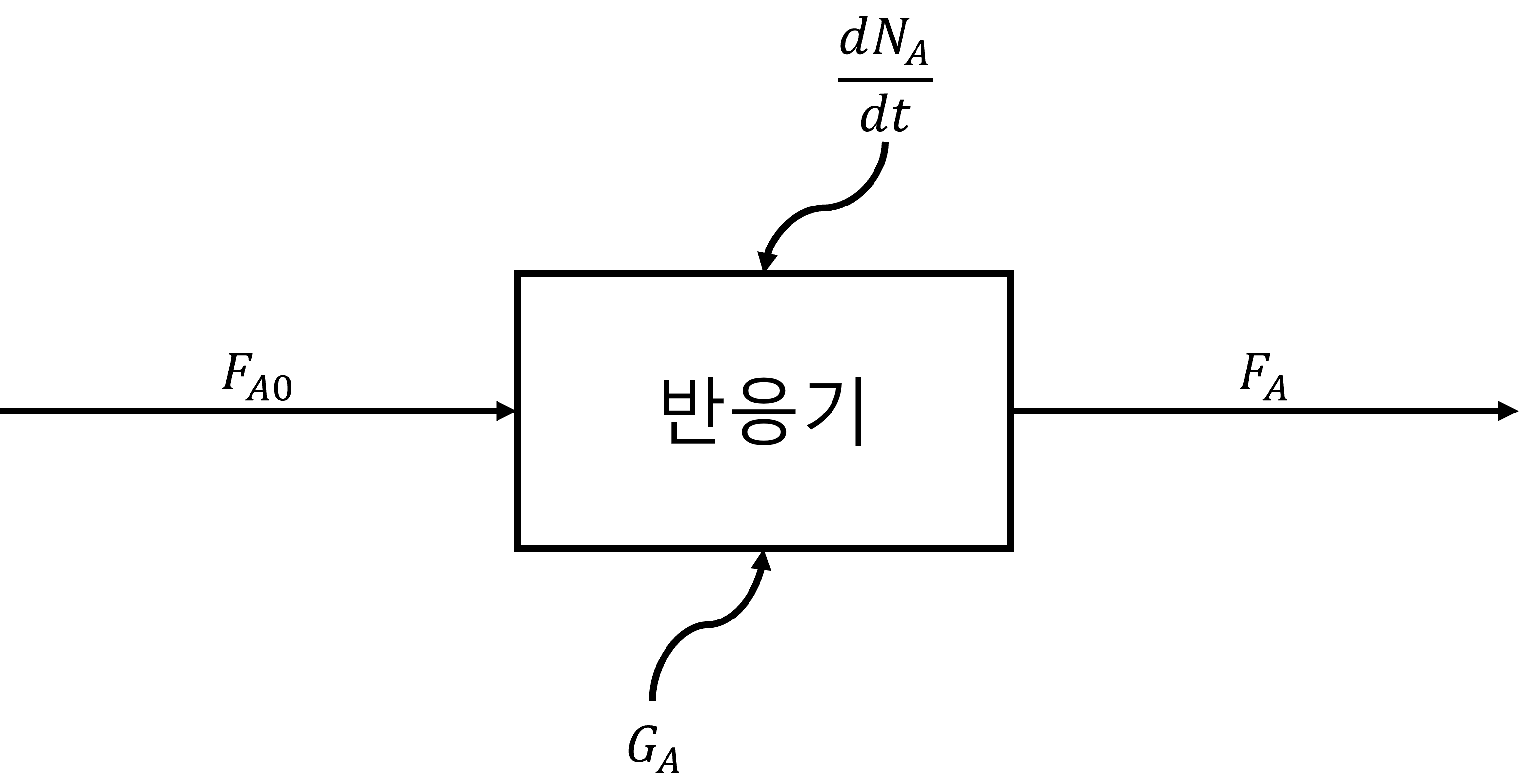
$$F_{A0}-F_{A}+G_{A}=\frac{\mathrm{d}N_{A}}{\mathrm{d}t}$$ 여기서 $F_{j}$는 j의 몰 유량(시간 당 j가 지나가는 양)을 의미하는 표현입니다. 앞으로도 많이 나올 표현인 만큼 기억해 주세요!
여기까지 하면 한 가지 의문이 들 수 있습니다. 과연 $G_{A}$는 무슨 뜻일까요? 앞서 반응 속도 $r_{A}$가 단위 부피 당 반응 속도라는 이야기를 다뤘습니다. 이걸 이 식에 적용하려면 전체 부피로 반응 속도를 바꿔 주어야 합니다. 그렇기 때문에 $G_{A}=r_{A}\times V$라는 값을 새로 나타내서 식을 적은 것이라고 이해하면 됩니다. 반응기의 각 지점 별로 반응 속도가 다르다면 적분을 사용해서 $G_{A}=\int^{V}{r_{A}\space \mathrm{d}V}$로 나타낼 수 있습니다. 이에 따라 최종적으로 우리가 기억해야 하는 일반적인 몰 수지식은 다음과 같이 나타납니다. $$F_{j0}-F_{j}+\int^{V}{r_{j}\space \mathrm{d}V}=\frac{\mathrm{d}N_{j}}{\mathrm{d}t}$$ 지금은 어색할 수 있지만, 앞으로 반응공학을 배우면서 계속 만나게 될 식인 만큼 일반적인 몰 수지식과 친숙해지도록 해 봅시다!
반응기의 종류
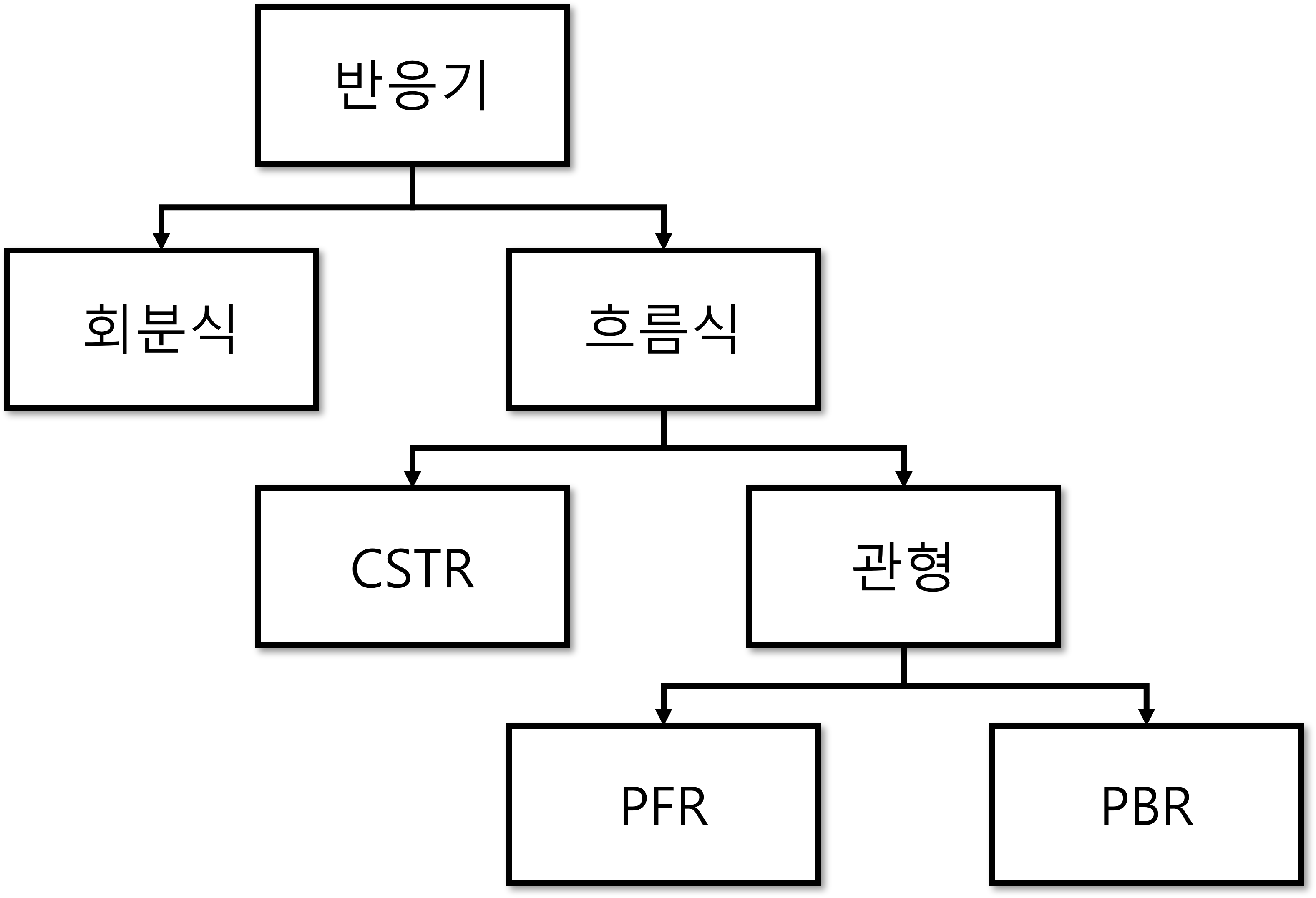
이렇게 반응공학 공부를 위한 모든 준비를 마쳤습니다. 이제 오늘의 하이라이트, 반응기의 종류로 넘어가 봅시다! 오늘 다룰 반응기의 종류는 4가지가 있습니다. 아래 그림처럼 종류를 나눠볼 수 있는데요, 예시와 함께 하나씩 지금부터 알아보도록 해요!
1. 회분식(batch)
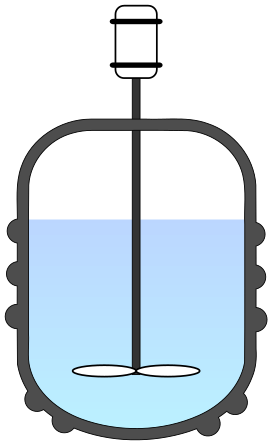
회분식 반응기는 반응기로 들어가는 물질도, 반응기에서 나오는 물질도 없이 반응기에 반응물을 담아 반응이 일어납니다.
GYassineMrabetTalk✉, Public domain, via Wikimedia Commons1
설탕(수크로스, sucrose)는 수크레이스(sucrase)가 있을 때 상온에서 분해 반응을 진행한다고 합니다.2 이 반응을 회분식 반응기에서 진행한다면 위 그림과 같이 유입과 유출이 없는 반응기에 반응물만 차 있는 모습을 볼 수 있겠네요. 이 경우에 sucrose를 반응물 A라고 하고, 반응물 A에 대해서 몰 수지식을 세워 봅시다.
유입과 유출은 없으므로 $F_{A0}$와 $F_{A}$는 0이 됩니다. 만약에 반응기에서 완벽하게 물질이 섞인다면 모든 위치에서 반응 속도가 동일함을 알 수 있으니까 적분을 풀면 다음과 같은 몰 수지식을 얻을 수 있습니다!$$\frac{\mathrm{d}N_{A}}{\mathrm{d}t}=r_{A}V$$ 이 식은 회분식 반응기의 설계방정식(design equation)이라고 합니다! 이때 만약 처음에 1몰 만큼의 설탕을 넣고, 반응을 진행했을 때 0.16몰 만큼이 남았다면, 얼마나 시간이 걸릴까요? 이 문제를 해결하기 위해서는 위 수지식을 적분해야 합니다! 시간을 좌변에 두고 나머지를 우변으로 이항하면 $$\mathrm{d}t=\frac{\mathrm{d}N_{A}}{r_{A}V}$$ 로 정리되고, 구하고자 하는 시간 $t_{1}$은 $$t_{1}=\int_{0.16}^{1}{\frac{\mathrm{d}N_{A}}{-r_{A}V}}$$ 으로 구할 수 있습니다.
용어 정리
아쉽지만 나머지 반응기의 종류는 분량 상 다음 게시물에서 알아보도록 해요! 오늘은 여러분들과 함께 일반적인 몰 수지식과 회분식 반응기를 공부했는데요, 어려운 부분이 있거나 궁금한 부분, 제안 사항이 있다면 답글로 남겨주세요!!
오늘 사용한 용어는 아래 표를 참고해 주시면 감사하겠습니다.
<사용 용어 표>
| 한국어 명칭 | 영어 명칭 |
|---|---|
| 반응 속도 | reaction rate |
| 몰 수지 | mole balance |
| 일반적인 몰 수지식 | general mole balance equation |
| 몰 유량 | molar flow rate |
| 회분식 반응기 | batch reactor |
| 흐름식 반응기 | flow reactor |
| 연속 교반 탱크 반응기(혼합 흐름 반응기) | CSTR, continuous stirred tank reactor |
| 관형 반응기 | tubular reactor |
| 플러그 흐름 반응기 | PFR, plug flow reactor |
| 충전층 반응기 | PBR, packed bed reactor |
| 설계방정식 | design equation |
- Batch Reactor, Wikipedia, https://en.wikipedia.org/wiki/Batch_reactor 참조 ↩︎
- Octave Levenspiel 교수님의 저서 Chemical Reaction Engineering, 3rd edition의 Chapter 27 연습문제에서 상황을 참조하였습니다. 나중에 bioreactor에 대해 공부할 때 Batch reactor에 상황을 적용하는 연습을 할 분들은 참고해 주세요. ↩︎
'지난 연재물 - 화학생물공학 > [반응공학] 예시로 알아보는 반응공학' 카테고리의 다른 글
| 예시로 알아보는 반응공학: 3번째, 반응 속도와 화학양론 (2) | 2022.08.01 |
|---|---|
| 예시로 알아보는 반응공학: 2번째, 전화율 & 반응기의 크기(2) (5) | 2022.04.08 |
| 예시로 알아보는 반응공학: 2번째, 전화율 & 반응기의 크기 (1) (1) | 2021.12.19 |
| 예시로 알아보는 반응공학: 1번째, 몰 수지(2) (1) | 2021.12.02 |
| 예시로 알아보는 반응공학 - 화학 공장에서는 무슨 일이? (1) | 2021.11.11 |




댓글