#7. Fourier Series(2. extension)

사진 출처

- 이분이 바로 푸리에!

Fourier series - 복습

저번 포스팅에서는, 가장 기본적인 Fourier series가 어떻게 생겼는지 살펴봤습니다. 아주아주아주 특수한, $2\pi$의 주기를 갖는 경우에 대한 급수를 아래와 같이 표현했었죠.

$$\begin{align}f(x) &= a_0 + \sum_{n=1}^\infty (a_n \cos nx + b_n \sin nx)\\ a_0 & = \frac{1}{2\pi} \int_{-\pi}^\pi f(x) dx \\ a_n & = \frac{1}{\pi} \int_{-\pi}^\pi f(x) \cos nx dx \\ b_n &= \frac{1}{\pi} \int_{-\pi}^\pi f(x) \sin nx dx \end{align}$$

오늘은 좀 더 일반적인 경우에 대해 살펴볼겁니다 바로 시작해 볼까요?

Fourier series - 주기가 $2\pi$가 아니라면

항상 주기가 $2\pi$인것은 아닐겁니다. 주기가 그냥 2일 수도 있고, $e$일 수도 있습니다. 2의 e승... e의 2승...? 이런 일반적인 경우에 대한 이야기를 더 해주기 위해, 우리는 위에 있는 저 식에 살짝 치환을 해줘서 조금 고쳐볼거에요. 헷갈리니까 잘 따라와봅시다.

우리가 원하는 주기?

원래의 fourier series 의 주기는 $\frac{2\pi}{n}$였습니다. 우리가 원하는 주기는, $\frac{2L}{n}$라고 가정해볼까요?

• 여기서 잠깐…
  삼각함수의 주기는 어떻게 구하던가요? $\cos ax$의 주기는, $\frac{2\pi}{a}$와 같이 구하던 것, 당연히 알고 있죠?

지금 $x$가 그냥 그대로 붙어있는 상태로는 절대 주기를 바꿀 수 없습니다. 여전히 $\frac{2\pi}{n}$으로 나오겠죠. $x$ 앞에 뭔가 붙어있어야 합니다. 그 ‘뭔가’를 $\alpha$라고 두고, 그대로 다시 집어넣어줍시다.
$$f(\alpha x) = a_0 + \sum_{n=1}^\infty (a_n \cos n\alpha x + b_n \sin n\alpha x)$$
뭐..그냥 갖다 넣은거니까요! 그러면, 이놈의 주기는 조금 얘기가 달라집니다. 암산이 되죠? $\frac{2\pi}{n\alpha}$가 됩니다. 이것이 우리가 원하는 주기인 $\frac{2L}{n}$이 되려면, 아래와 같은 수식을 만족해야합니다.

$$\frac{2\pi}{n\alpha} = \frac{2L}{n}$$
그러면, $\alpha$, 즉 $x$앞에 붙어있던 놈은 뭐가되나요?

$$\alpha = \frac{\pi}{L}$$
가 됩니다. 이걸 다시 대입해줍시다.

얻어진 식

$$f(\frac{\pi}{L}x) =a_0 + \sum_{n=1}^\infty (a_n \cos \frac{n\pi}{L} x + b_n \sin \frac{n\pi}{L} x)$$

그러면 좌변을 일단 무시해봅시다. 모양이 좀 안예쁘거든요. 우변만 생각해보면, 저 모양은 분명 주기가 $\frac{2L}{n}$인 놈입니다. 그러니, 저 모양을 그대로 fourier 식이다! 라고 정하자는 거죠.

$$f(x) = a_0 + \sum_{n=1}^\infty (a_n \cos \frac{n\pi}{L} x + b_n \sin \frac{n\pi}{L} x)$$

ㅋㅋㅋㅋ 이렇게 넘어오는 과정이 좀 당황스러울겁니다. 좌변끼리는 아무~런 상관이 없다는 것만 신경써주시면 됩니다!
걍 이렇게 정의를 해서, 주기가 $2\pi$가 아닌 함수에 대한 일반적인 얘기를 하겠다는거니까요. $L=\pi$를 대입해서 주기가 $\frac{2\pi}{n}$이 나오도록 하면, 이전 포스팅에서 봤던 Fourier series 와 식이 같습니다. 다시 말하면, 더 일반적인 경우에 대한 Fourier series 를 새로 정의한다…정도로 이해하면 되겠네요!

• 주기가 $\frac{2L}{n}$인 함수에 대한 일반적인 Fourier series
  $$f(x) = a_0 + \sum_{n=1}^\infty (a_n \cos \frac{n\pi}{L} x + b_n \sin \frac{n\pi}{L} x)$$

사실…

Kreyzig 책을 보면 이 부분이 별로 와닿지 않습니다. ㅋㅋㅋㅋㅋㅋㅋ 수알못이 책 저자를 까다니...ㅠㅠㅠ
$x= \frac{p}{2\pi} \nu$요런 치환을 도입하기 때문이죠. 오히려 이 방법이 더 엄밀할 수도 있어요! 하지만 저는, 굳이 $\nu$를 대입했다가 괜히 포스팅에서 헤메게 될까봐 도입하지 않은 것 뿐입니다. 일단 저런식으로 이해만 해두고, 슬슬 따라와보시면 되겠습니다! ㅋㅋㅋ

계수 구하기

그러면 새로운 형태의 Fourier series 를 구했으니 계수들도 다시 새로 다 구해야합니다…………는 아니구요, 그냥 우리가 기존에 구해둔 공식의 삼각함수 뒷 부분에 $x$대신 $\frac{n\pi}{L}x$를 대입하면 되겠습니다. 증명은 이전 포스팅과 똑같이 하시면 되구요, 생략하고 결과만 뙇! 표시해볼게요 ^^

$$\begin{align} a_0 &= \frac{1}{2L} \int_{-L}^L f(x)dx \\ a_n &=\frac{1}{L} \int_{-L}^L f(x) \cos \frac{n\pi}{L}x dx \\ b_n &= \frac{1}{L} \int_{-L}^L f(x) \sin \frac{n\pi}{L}x dx\end{align}$$

정리

주기가 $2\pi$가 아닌 일반적인 함수에 대하여,
$$\begin{align} f(x) &= a_0 + \sum_{n=1}^\infty (a_n \cos \frac{n\pi}{L} x + b_n \sin \frac{n\pi}{L} x) \\a_0 &= \frac{1}{2L} \int_{-L}^L f(x)dx \\ a_n &=\frac{1}{L} \int_{-L}^L f(x) \cos \frac{n\pi}{L}x dx \\ b_n &= \frac{1}{L} \int_{-L}^L f(x) \sin \frac{n\pi}{L}x dx\end{align}$$

이 때, 적분 범위는 한 주기 내부 전체!!!!입니다.

Fourier series - odd / even

그러면, 제가 기다리고 기다렸던 odd/even(기함수/우함수)얘기를 할 수 있을 것 같네요. 이게 뭔지는 다들 아시죠?

odd/even function의 정의와 성질

• odd function (기함수)
  $$f(-x) = -f(x)$$

• even function (우함수)
  $$f(-x) = f(x)$$

저는 고등학교때, 기함수는 $-$부호가 함수 앞으로 기어나와서 기함수고, 우함수는 $-$부호가 없어진다고 해서 우함수…라는 신박한 암기법을 들은 기억이 있습니다. ㅋㅋㅋㅋㅋㅋㅋ
여튼, $-$부호에 대한 처리 방법 때문에 기함수는 원점대칭, 우함수는 $y$축 대칭이라는 아주 중요한 성질을 갖습니다. 또, 함수끼리의 곱에 대해서는 이런 성질이 있죠.

• (우함수) $\times$ (우함수) = (우함수)
  (우함수) $\times$ (기함수) = (기함수)
  (기함수) $\times$ (기함수) = (우함수)

정의를 그대로 가져와서 두 함수를 곱해보면 결과는 쉽게 얻을 수 있습니다. 대표적인 우함수로는 $\cos x$정도가 있을거고, 대표적인 기함수는 $\sin x$정도가 있겠네요. 왜 이 얘기를 꺼냈는지 감이 잡히죠?

잠시, 그런데 기함수는!! 원점에 대해 대칭입니다. 한 주기째 통째로 적분을 해버리면 고대로 0이 되어 날아가버리는, 아주 간편한 녀석이죠. 0은 아주 편한 숫자니까요. 이 중요한 성질들을 머릿속에 두고, 항을 하나씩 지워봅시다.

간소화

솔직히, 저 식을 어떻게 다 외우고 다닙니까. 외우지 않더라도, 컴퓨터 입장에서는 쓰지도 않을 식을 불러오고, 계산해서, 0이 나오는….과정을 굳이 하고싶지 않을거구요. 그래서, 과감하게 기함수와 우함수에 대한 조건을 추가합니다.

• $f(x)$가 odd function(기함수)라면
  우함수인 $\cos x$와의 곱이 기함수가 될겁니다. 그러니 $a_n$을 이루는 항이…..
  $$\int_{-L}^L f(x) \cos \frac{n\pi}{L} x dx =0$$ 으로 되어 지워지겠죠.
  마찬가지로, $a_0$을 이루는 항도
  $$\int_{-L}^L f(x) dx =0$$
  으로 사라질겁니다.

• $f(x)$가 even function(우함수)라면
  기함수인 $\sin x$와의 곱이 기함수가 되겠죠? 그러니 $b_n$을 이루는 항은
  $$\int_{-L}^L f(x) \sin \frac{n\pi}{L}xdx= 0$$
  으로 날아갈겁니다.

결론적으로는

$f(x)$가 odd function 인 경우에는,
$$f(x) = \rlap{//}{a_0} + \sum_{n=1}^\infty (\rlap{//}a_n \cos \frac{n\pi}{L} x + b_n \sin \frac{n\pi}{L} x)$$ 가 되어 결국 $b_n$과 $\sin$만 남게 됩니다.
$$f(x) = \sum_{n=1}^\infty b_n \sin\frac{n\pi}{L}x$$
싸인! 만 남아있네요. 그래서 우린 이걸 Fourier Sine Series라고 부를겁니다.

반대로, $f(x)$가 even function 인 경우에는,
$$f(x) = a_0 + \sum_{n=1}^\infty (a_n \cos \frac{n\pi}{L} x + \rlap{//}b_n \sin \frac{n\pi}{L} x)$$
가 되어 결국 $a_n$과 $\cos$, $a_0$이 남게 되겠죠. 정리하면,
$$f(x) = a_0 + \sum_{n=1}^\infty a_n \cos \frac{n\pi}{L}x$$
눈치챘죠? 우린 이걸 Fourier Cosine Series라고 부를겁니다.

그래서, 우함수다! 라는 확신이 선다면 과감하게 $b_n$을 계산하는데에 힘을 1도 쏟지 않아도 될거다…라는 얘기죠. 이렇게 머리를 쓰는 겁니다 ^0^ㅋㅋ

Fourier series extension

그런데 우리의 Fourier 에게는 하나의 과제가 더 남았습니다. 바로 Odd/Even function extension 인데요, 처음 봤을때는 이런 생각이 들 수도 있습니다.

• 멀쩡한 함수를 왜 굳이 $y$축 대칭, 원점 대칭을 시켜서 저멀리 쭉쭉 보내는가….

맞습니다. 저도 그랬거든요. 그래서 이번 포스팅을 위해 한참을 들여다보고 찾아봤습니다.그래서 포스팅이 늦게 올라온 건 변명...

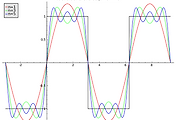
생각할 것이 하나 있습니다. $\sin, \cos$함수는, 주기함수입니다. 다시 말해서, 아래와 같은 모양으로 주어진 함수가 있다고 치면….

그림 출처(수정된 그림)

사실 이런 함수를 정말 많이 얻게 될겁니다. 가로축은 보통 시간이거나 위치일텐데, 이 값들은 ‘양수범위’에서 일반적으로 측정가능한 값들이니까요. 이 함수를 그대로 Fourier series 를 통해 근사해볼까요? 0부터 $L$까지만 나타내야 하는걸까요?…..

바로 그런 문제 때문에 나온 해결책이, extension 입니다. 보통 실험 데이터 자체는 주기함수적 성질을 가지는 것이 아니라, 딱 interval 을 가지고 측정한 후 끝! 이거든요. 그래서 우리는 Fourier의 모양에 맞게, 양쪽으로 쭉쭉 복붙을 한 다음 입맛에 맞게 계수를 가져오면 그만입니다.

그런데 막상 복붙을 하려 보니, 아무렇게나 복붙을 하고 주기를 만들면 상당히 $a_0, a_n, b_n$들이 골룸해질 것 같다는 겁니다. 그래서 딱 이 두가지 extension 을 가장 편리한 경우로 생각하고 사용할 겁니다.

1. Fourier Odd extension
2. Fourier Even extension

1번의 경우 $\sin$함수만을 사용해서 확장할 수 있을 겁니다. Fourier sine series가 되는거죠. 마찬가지로, 2번의 경우 $\cos$함수만을 사용해서 확장할 수 있고, 이건 Fourier cosine series 가 됩니다. 실제 예시는 아래 두 그림을 참고하시면!

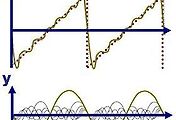
Odd extension 의 경우

그림 출처(수정된 그림)

Even extension 의 경우

그림 출처(수정된 그림)

이렇게, 한 주기[$-L$~$L$]안의 모양을 예쁘게 만들어 놓은 다음 좌우로 복붙을 하면 됩니다. 주기함수로 근사할거니까요.

그래서, extension 을 하는 이유는,
- 양의 범위에서 주기함수가 아닌 형태로 얻어진 어떤 data에 대한 근사를 하고 싶으니까,
- 필요한 형태(아마 필요한 삼각함수가 될 가능성이 높죠!)에 따라 odd, even으로 한 주기 내의 모양을 만들어 둔 후
- 쫙쫙 잡아늘려서 삼각함수 형태로 근사하기 좋게 만들어두면
- 누이좋고 매부좋고!

정도로 요약해볼 수 있겠네요. 바로 이것 때문에 Fourier sine, cosine series를 따로 만들어놓는 겁니다.

다음 시간 예고

뒷 부분에서 제가 겪었을 멘붕을 여러분은 잘 해소하셨길 빕니다 ㅠㅠㅠㅠ 다음시간에는, Fourier series로 신나게 근사하는 것이 과연 얼마나 정확할지에 대한 이야기를 해보려고 해요. 신나게 근사를 한답시고 했는데 진짜 $n=100$이상이 되면 $f(x)$와 전혀 다른 모양으로 전개가 되어 버린다거나…..하면 곤란하겠죠ㅠㅠ

이걸 계산하는 과정에서 굉장히 유명하고 중요한 그놈의 베쎌을 여기서도 또 봅니다 여기서도 공식을 몇 가지 만나게 될 겁니다. 다음 포스팅에서는 식이 다소 길고 머리가 아플 수도 있으니 충분히 식들에 익숙해진 상태로 만날 수 있길 빕니다. 그럼 다음포스팅에서 봐요!