안녕하세요! 공우 15기 전기정보공학부 20학번 김유신입니다. 전기정보공학부의 전공 선택 과목인 '알고리즘의 기초’에 대해 소개하겠습니다.
1. 과목에서 배울 수 있는 내용
1.1 과목의 전반적인 개요
알고리즘의 기초는 권장학기가 3학년 2학기인 컴퓨터 분야의 교과목으로, 권장 선 이수 교과목은 자료구조의 기초입니다. 알고리즘의 기초에서는 이름에서 알 수 있듯 복잡한 문제를 체계적으로 분석하고 해결하는데 필요한 여러 알고리즘들을 다룹니다. 학생들은 실생활에서 접하는 다양한 문제를 풀어내는데 기초가 되는 알고리즘들을 통해 문제를 정형화하고, 정형화한 문제를 풀어내는 능력을 배울 수 있습니다. 알고리즘의 기초 과목의 목표가 다양한 알고리즘의 소개인 만큼, 한 학기동안 10개 남짓한 주제 키워드와 각 키워드를 대표하는 알고리즘들을 순서대로 접하게 됩니다.
1.2 키워드 별 개념 설명
가. 알고리즘 분석
알고리즘을 분석하는 가장 중요한 요소는 Running Time입니다. Worst case running time은 가능한 범위에서 가장 긴 시간을, Average case running time은 랜덤한 입력에 대해 평균적으로 걸리는 시간을 분석합니다. 대체로 Worst case가 더 중요하게 다뤄지고, 주요 알고리즘들은 작은 계수와 차수를 가지는 polynomial running time을 가지는 경우가 많습니다. Running time의 bound를 나타내기 위해서 Asymptotic Order of Growth를 사용하는데, 예를 들어 Upper bounds의 경우, 알고리즘의 표현식 이면 ’ is '과 같이 표현합니다. 자주 쓰이는 Running Time은 등이 있습니다.
나. 그래프
Undirected graph 는 꼭짓점 nodes와 꼭짓점들을 잇는 edges로 이루어진 방향성이 없는 그래프를 의미합니다. Directed graph는 edges에 방향이 있는 그래프를 의미하고, 그래프를 표현하는 방법은 nodes 사이의 edge 유무를 표시한 Adjacency Matrix, indexed array를 활용한 Adjacency List가 있습니다. 두 개 이상의 node를 지나는 경로를 Cycle, Cycle이 없이 연결되어 있는 undirected graph를 tree라고 정의합니다.
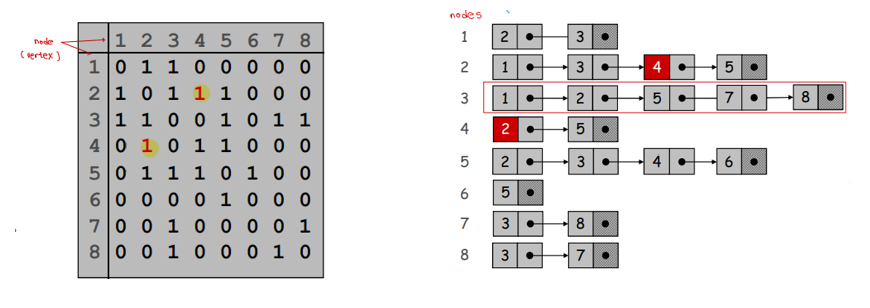
한편, 그래프에서는 두 노드가 서로 연결되어 있는지 또는 두 노드를 잇는 가장 짧은 경로가 무엇인지 등을 다루는 문제가 중요합니다. Breadth First Search (BFS) Algorithm에서는 시작 노드로부터 연결된 모든 노드를 한 layer씩 쌓아 나가는 방식으로 연결성을 찾습니다. Adjacency list를 이용해 구현하면 BFS 알고리즘은 의 running time을 갖습니다. Directed graph에서 임의의 노드 u, v에 대해 u에서 v로 가는 경로, v에서 u로 가는 경로가 모두 존재하면 Strong Connectivity가 있다고 말합니다. 이는 원래 그래프와 원래 그래프의 edge 방향을 모두 반대로 한 reverse oriented graph에서 각각 BFS를 적용하여 확인합니다.
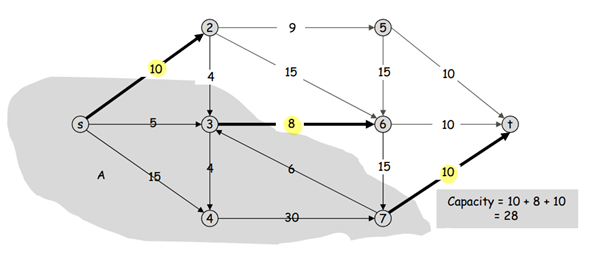
Parallel edges가 없는 directed graph에서 각각의 edge에 weight가 부여된 형태의 그래프를 Flow Network라 하며, 시작점을 source s, 도착점을 sink t로 정의합니다. s-t cut은 partition A, B를 생성하고, A에서 B로 향하는 weights들의 합을 Capacity라고 얘기합니다. 이런 Flow Network에서는 가장 작은 capacity를 찾는 minimum cut 문제, 흘러가는 가장 큰 값의 flow를 찾는 maximum flow 문제를 생각할 수 있고, 추가적인 path를 연결해 문제를 푸는 Ford-Fulkerson 알고리즘이 존재합니다.
다. Greedy algorithm
Greedy algorithm은 문제를 단계적으로 분리하고, 각 단계마다 그 순간의 최선의 Solution을 선택하면서 최종적인 Solution을 만들어내는 알고리즘입니다. 각 단계에서 선택한 최선의 Solution을 Local Optimum, 최종적인 Solution을 Global Optimum으로 생각할 수 있습니다. 시간 에 시작해서 에 끝나는 여러 작업들이 있을 때, 서로 겹치지 않는 가장 많은 작업들을 선택하는 Interval Scheduling 문제가 Greedy Solution을 가지는 대표적인 예시입니다. 이 문제를 풀기 위해서는 먼저 작업들을 끝나는 시간이 이른 순서대로 배열하고, 가장 일찍 끝나는 작업을 선택합니다. 이후, 이전 작업과 겹치지 않으면서 가장 일찍 끝나는 작업을 반복해서 선택하면 이 문제의 Global Optimum을 구할 수 있습니다. 배열 과정에서 필요한 시간이 , 선택 과정에서 필요한 시간이 이므로, 알고리즘 수행이 필요한 총 시간은 입니다. 한편, Greedy Solution이 not optimal임을 가정하고 작업을 배열했을 때, Greedy Solution보다 나쁜 상황만 생기는 모순을 이용해 Greedy Solution이 실제 Optimal임을 증명할 수 있습니다.
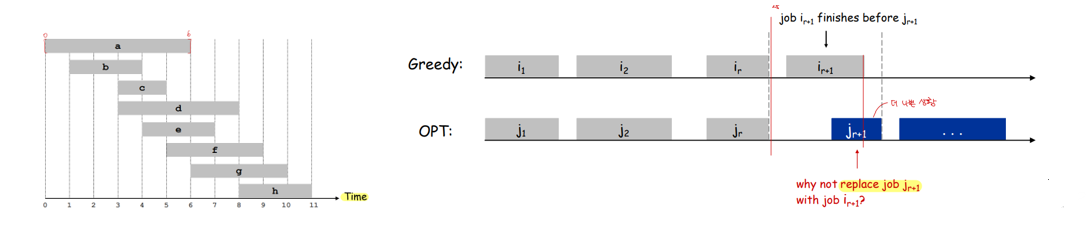
이외에도, Interval Partitioning, Scheduling to Minimize Lateness, Optimal Caching, Dijkstra’s algorithm 등의 문제에 Greedy algorithm을 적용할 수 있습니다.
라. Divide-and-Conquer
Divide-and-Conquer은 문제를 작은 문제로 분할하여 문제를 해결하는 방법을 통칭하는 알고리즘입니다. Divide-and-Conquer은 세 단계로 이루어지는데, (1) Divide, 원래 문제를 분할하여 비슷한 유형을 가지는 작은 문제로 분할이 가능할 때까지 나누고, (2) Conquer, 나뉜 각 문제를 재귀적인 방법을 통해 해결하고, (3) Combine, 해결한 문제를 통합하여 원래 문제의 Solution을 구합니다. Divide-and-Conquer은 Divide 과정을 잘 설계하는 것이 무엇보다 중요하고, 재귀 알고리즘을 사용하여 수행하는 경우가 대부분입니다. 실행 과정에서의 장점은 Top-down 방식이므로 직관적이고, 병렬적으로 작은 문제들을 처리할 수 있다는 점입니다. 단점은 재귀 실행 과정에서 오버헤드나 Stack Overflow 등을 제어할 수 없다는 점입니다.
가장 대표적인 Divide-and-Conquer 문제의 예시는 Merge Sort입니다. 하나의 입력 리스트를 균등한 크기의 부분 리스트로 반복적으로 분할한 다음, 충분히 작은 크기의 부분 리스트에서부터 정렬을 시작하여, 정렬된 부분 리스트들을 하나의 리스트에 합병하는 방식으로 Solution을 구할 수 있습니다. 각 단계의 정렬에 필요한 시간은 , 총 단계가 만큼 존재하므로, 알고리즘 수행이 필요한 총 시간은 입니다.
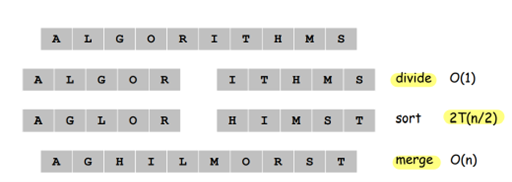
이외에도, Counting Inversions, Closest Pair of Points 등의 문제에 Divide-and-Conquer 알고리즘을 적용할 수 있습니다.
마. Dynamic programming
Dynamic programming은 문제를 작은 문제로 나누고, 작은 부분 문제들의 Solution이 반복되는 것을 이용해 전체 Solution을 구하는 알고리즘입니다. 작은 문제가 반복해서 나타나고, 같은 문제는 매번 같은 Solution을 가지는 조건이 있으면 Dynamic programming으로 Optimal Solution을 구할 수 있습니다. 이때, 모든 작은 문제는 한 번씩만 풀고, 문제에서 얻은 정답을 어딘가에 저장해둔 다음, 다시 그 문제를 마주치면 앞서 메모한 결과를 참조하는 Memoization을 사용합니다. 간단한 예로, 피보나치 수열의 5번째 항을 구하기 위해서는 4번째 항과 3번째 항이 필요하고, 4번째 항을 구하기 위해서는 3번째 항과 2번째 항이 필요합니다. 두 경우에서 모두 같은 3번째 항이 필요하고, 이런 구조를 작은 문제의 반복으로 볼 수 있습니다.
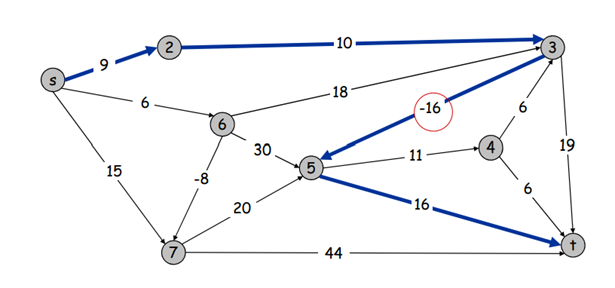
Directed graph 에서 각 edge에 음의 weights을 포함한 weights가 있을 때, 두 노드 사이의 가장 짧은 거리를 찾는 문제를 생각해봅시다. Greedy algorithm의 일종인 Dijkstra 알고리즘은 음의 weights를 처리하지 못해 Optimal Solution을 얻을 수 없습니다. 한편, 두 노드 사이에 음의 cost를 갖는 cycle이 존재한다면 두 노드 사이의 가장 짧은 거리는 음의 무한대가 되고, 존재하지 않는다면 이 문제는 하나의 Solution을 가집니다. 이하의 edges를 지나는 두 노드 사이의 최소 거리를 라고 하면 또는 v에서 도달하는 노드 w에 대해 (: 노드 v와 w 사이의 cost) 입니다. 이를 이용하면 전체 문제에 대한 Solution을 구할 수 있고, 가 개의 값을 따라 변하는 동안 각각 시간이 필요하므로, 전체 시간은 , 작은 문제의 정답을 저장하기 위한 공간은 이 필요합니다. 이를 Bellan-Ford algorithm이라고 얘기하며, Dijkstra와 주요한 차이점은 매 반복마다 해당 노드에서 연결된 모든 edges을 다 확인한다는 점입니다.
이외에도, Weighted Interval Scheduling, Segmented Least Squares, Knapsack Problem, Negative Cycles in a Graph 등의 문제에 Dynamic programming 알고리즘을 사용할 수 있습니다.
사. 학기 후반부에는 Np와 Np-complete의 개념을 다루고, Polynomial-time 내에서 한 문제를 이미 Solution을 알고 있는 다른 문제로 변형하여 Solution을 얻는 Reduction by Equivalence, Reduction from Special to General 등의 방법을 접하게 됩니다. 또, 이를 이용하여 Load Balancing, Center Selection, Weighted Vertex Cover와 같은 유명한 문제의 Optimal Solution을 구하는 방법을 배웁니다. 더 자세한 내용은 알고리즘의 기초 수업에서 공부해보기를 추천합니다!
2. 선배의 조언
알고리즘의 기초는 권장 선 이수 과목으로 자료구조의 기초를 가지고 있습니다. 다만, 프로그래밍방법론 수준의 코딩 기초를 이해하고 있다면 순서를 꼭 지켜야 할 필요는 없다고 생각합니다. 일반적으로는 자료구조의 기초 전반부에서 다루는 내용이 알고리즘의 기초를 이해하는데 도움을 줍니다. 교수님에 따라 다르지만, 자료구조의 기초 후반부의 내용은 알고리즘의 기초와 겹치는 내용도 많습니다. 따라서, 자료구조의 기초와 알고리즘의 기초를 같은 학기에 수강하는 것도 관련 분야의 기초를 탄탄히 다지기에 좋은 선택입니다. 즉, 가장 무난한 선택은 알고리즘의 기초를 자료구조의 기초와 함께 2학년 2학기에 수강하거나, 3학년 1학기에 수강하는 것입니다. 다른 과목을 공부하는데 기초가 되는 내용을 많이 담고 있는 만큼 늦어도 3학년 2학기에 수강하고, 이를 활용해 전기정보공학부의 심화 전공 과목들을 수강하기를 추천합니다.
알고리즘의 기초에서는 수많은 새로운 단어와 개념이 수업 내내 스쳐 지나가기 때문에 각 주제 키워드 별로 큰 흐름을 이해하고 난 후, 세부적인 알고리즘의 동작을 살펴보는 것이 중요합니다. 각각의 알고리즘의 조건이나 구현 과정에만 집중한다면 배우는 모든 내용을 외우는 것이 최선의 공부 방법입니다. 하지만, 알고리즘의 기초 과목을 수강하는 진정한 목적은 달성하지 못할 가능성이 높습니다. 강의에서 다룬 내용을 모두 영원히 기억할 수는 없을 뿐만 아니라, 새로운 알고리즘을 다루고 문제를 풀어내기 위해 아이디어를 응용하고 확장하기 어려울 것이기 때문입니다. 따라서, 각 주제에서 등장하는 중요한 아이디어와 그런 생각이 등장하게 된 이유를 충분히 이해하고, 디테일한 부분들은 시험 기간에 집중하는 방식을 추천하고 싶습니다.
한편, 교수님에 따라 문제를 접하고 알고리즘을 적용하여 정답을 얻는 큰 흐름 가운데서 어느 과정을 중요하게 배울지 달라지곤 합니다. 예를 들어 문제를 분석하고, 변형하여 해당 알고리즘에 접근하는 과정, 실제 알고리즘을 적용하여 문제의 정답을 알아내는 과정, 알고리즘을 적용하고 얻어낸 결과가 최적의 결과임을 증명하는 과정 등 다양한 과정이 포인트가 될 수 있겠죠. 또, 이론적인 분석을 중요하게 여기시는지, 코딩을 통한 알고리즘의 구현과 실행을 중요하게 여기시는지에 따라 나오는 과제의 스타일도 완전히 달라지게 됩니다. 한 학기 내내 코딩과 씨름하게 될 수도, 한 학기 내내 Optimality를 계산하게 될 수도 있죠. 알고리즘의 기초를 선택해서 들을 수 있는 상황이라면, 이전에 나온 과제나 강의평을 확인해보고 본인이 중요하게 생각하는 부분과 맞는 강의를 선택하기를 추천합니다.
3. 진로 선택에 도움되는 점
알고리즘의 기초는 컴퓨터 분야를 전공하고자 한다면 필수적으로 알아야 하는 내용을 다루고 있고, 컴퓨터 분야를 전공하지 않더라도 알아 두면 좋은 내용을 많이 포함하고 있습니다. 모든 엔지니어는 본인의 전공 분야에서 문제를 해결하는 사람이기 때문에 문제 해결에 도움을 주는 도구를 많이 가지고 있다면 큰 도움이 되겠죠? 다양한 알고리즘을 접하고 다뤄보는 것은 이 같은 효과를 줄 수 있습니다. 또, 같은 문제라도 어떤 알고리즘을 적용하는지에 따라 문제를 다루는 방법이 완전히 달라지기 때문에 문제를 바라보는 시각을 키울 수 있는 효과도 있습니다. 따라서, 전기정보공학부에서 진로를 꿈꾼다면 알고리즘의 기초를 수강하거나, 기초적인 알고리즘을 꼭 공부해보면 좋을 것 같습니다.
4. 맺음말
알고리즘의 기초는 문제를 해결하기 위해 필요한 다양한 알고리즘을 다루는 과목으로, 많은 양의 지식을 빠르게 전달하는 과목입니다. 큰 흐름을 놓치지 않는 것이 무엇보다 중요하다고 생각하고, 관심이 가는 알고리즘의 디테일을 파헤쳐 보는 것도 좋은 공부가 되었습니다. 알고리즘의 기초를 들으면서 가장 고민했던 부분은 ‘내가 수많은 천재들이 설계한 알고리즘을 순서대로 익힐 수는 있지만, 실제 문제를 만났을 때, 적합한 알고리즘 또는 아이디어를 바로 떠올려 낼 수 있을까?’ 하는 부분이었습니다. 알고리즘의 기초 시험 문제를 맞닥뜨렸을 때, 많은 학생들이 벽을 느끼고 드랍을 결심하는 이유이기도 합니다. 하지만, 모든 순간을 버텨내고 한 학기를 마무리하면 어느새 여러 알고리즘을 자유롭게 더하고 빼서 활용할 수 있는 자신을 만날 수 있을 것입니다. 알고리즘의 기초를 통해 얻는 다양한 관점과 도구를 바탕으로 즐거운 전기정보공학부 생활이 되길 바랍니다!
5. 출처
Algorithm Design, Jon Kleinberg and Eva Tardos, Wesley, 2005.

'전공백서 > 전기정보공학부' 카테고리의 다른 글
| 전기정보공학부: 컴퓨터 시스템 프로그래밍 (1) | 2024.07.01 |
|---|---|
| 전기정보공학부: 로봇공학개론 (1) | 2024.06.30 |
| 전기정보공학부: 딥러닝의 기초 (1) | 2024.06.26 |
| 전기정보공학부: 디지털 시스템 설계 및 실험 (0) | 2024.06.26 |
| 전기정보공학부: 기초회로이론 및 실험 (0) | 2024.06.23 |





댓글