전기정보공학부: 기초회로이론 및 실험

  안녕하세요! 공우 14기 전기정보공학부 19학번 채범준입니다. 전기는 우주의 4가지 기본 상호작용 중 인류가 유일하게 정복한 상호작용이자, 우리 문명을 떠받치고 있는 중요한 지지대입니다. 여러분들께서는 인류가 전기를 어떤 방식으로 사용하고 있는지 궁금하지 않으신가요? 에너지와 통신, 가전, 이동수단 등의 여러 분야에서 전기가 사용되는 원리는 무엇일까요? 이 답은 다양한 기기들에 내장된 회로에서 찾을 수 있을 것입니다. 저는 전기정보공학부에서 회로에 대해 본격적으로 공부하는 첫 번째 과목인 “기초회로이론 및 실험”을 소개해보려고 합니다.

1. 과목 개요

  기초회로이론 및 실험 과목은 전기정보공학부 2학년 봄 학기에 개설되는 과목으로, 프로그래밍방법론과 함께 듣는 첫 전공필수 과목입니다.

  이 과목에서는 저항, 연산증폭기(Operational Amplifier, Op Amp), 인덕터, 커패시터로 이루어진 회로를 어떻게 분석하는지를 공부합니다. 회로를 해석하는 가장 기본적인 규칙으로는 Kirchhoff의 전류 법칙(KCL)과 전압 법칙(KVL)이 있으며, 수업 전반부에서는 이 두 규칙에 기반해 저항(R)으로 이루어진 직류 회로를 분석해 봅니다. 추가로 Op Amp를 이용해 간단한 산술연산을 하는 회로, 두 입력 전압 크기를 비교하는 비교기(Comparator) 회로를 만드는 방법도 알아봅니다.

  중반부로 넘어가면 에너지를 저장하는 소자인 인덕터(L)와 커패시터(C)에 대해 배우는데, 이들의 전압과 전류 사이 관계는 시간에 대한 미적분으로 기술됩니다. 따라서 L과 C가 달려 있는 회로를 분석하려면 KCL과 KVL을 적용하여 전압이나 전류에 대한 미분방정식을 얻어내고 이를 풀어내야 합니다. 추가로, 앞에서와 마찬가지로, Op Amp를 이용해 이번에는 전압을 미분하거나 적분하는 회로를 만드는 방법을 공부합니다.

  하지만 입력되는 전원이 사인파의 형태로 주어진 경우, 선형회로의 모든 전압과 전류는 궁극적으로(steady-state) 주파수가 똑같은 정현파(사인파) 형태로 나타나게 됩니다(R, L, C와 Op Amp로 구성되어 있는 회로는 선형회로입니다.) 이 경우에는 미분방정식을 풀지 않고도, 복소수 페이저로 주어지는 또다른 KCL과 KVL를 이용하여 회로 응답을 분석할 수 있습니다. 이렇게 회로의 정현파 정상상태를 분석하는 방법은 수업 후반부에서의 주요 학습목표입니다.

2. 간단히 살펴보는 과목 내용

2.1. R, L, C 소자들의 작동

  이 과목에서는 R, L, C 세 가지 수동소자(passive elements)들이 회로 안에서 어떻게 동작하는지 공부합니다. 저항(R)은 전기장을 따라 전하들의 이동하는 drift에 기반해 작동하는 소자로, 전압과 전류가 선형 비례 관계에 있다는 Ohm의 법칙를 따르게 됩니다. 인덕터(L)는 시간에 따라 변하는 자기장이 전기장을 만들어낸다는 Faraday의 법칙을 이용하는 소자입니다. 커패시터(C)는 전하가 전기장을 만들어낸다는 Coulomb의 법칙에 기반하여 작동하는 소자로, 전류가 전하량의 시간에 대한 미분이라는 점을 이용해 커패시터의 전압과 전류 사이의 관계를 유도할 수 있습니다. 사실 각 소자들의 물리적인 작동 원리는 이후 기초전자기학 등의 수업에서 배울 수 있으며, 여기서는 각 소자의 전압과 전류 사이의 관계를 익히는 것이 더욱 중요합니다.

그림 1. 저항(R), 인덕터(L), 커패시터(C)의 회로도 기호.

  R, L, C를 나타내는 기호, 그리고 R, L, C 양단 전압(V)과 소자를 통과하는 전류(I) 사이의 관계는 위의 그림에서 확인할 수 있습니다. 저항으로 이루어진 회로를 분석하는 방법은 과목 전반부의 중요한 학습 목표이며, L과 C는 시간에 따라 전압과 전류가 변하는 회로의 응답을 공부하는 과목 후반부에서 회로의 구성 요소로 등장하게 됩니다.

2.2. 전원 이해하기

그림 2. 회로에 사용되는 전원의 종류.

  회로를 작동시키려면 전압을 걸어주거나 전류를 흘려보내주어야 하며, 이것은 전원을 이용해 구현할 수 있습니다. 전원에는 그에 따라 전압원과 전류원 두 종류가 있으며, 한편으로 전원값이 회로 외부에서 결정되는지, 내부에서 결정되는지에 따라 독립전원과 종속전원으로도 분류됩니다. 회로도에서 전원들은 위 그림에 나타난 기호로 나타냅니다.

2.3. Kirchhoff의 회로 법칙

  회로도에서 도선이 모이는 점을 노드(node)라고 부르고, 도선과 소자로 둘러싸인 고리를 루프(loop)나 메쉬(mesh)라고 부릅니다. Kirchhoff의 전류 법칙(Kirchhoff’s Current Law, KCL)은 회로 내 노드에 대해서, 이 노드로 들어가는 모든 전류의 합은 이 노드에서 나오는 모든 전류의 합과 같다는 법칙입니다. 즉 노드에는 전하가 쌓일 수 없다는 전하량 보존 법칙이라고도 볼 수 있어요. Kirchhoff의 전압 법칙(Kirchhoff’s Voltage Law, KVL)은 루프를 따라 전압 강하를 전부 합해보면 0이 나와야 한다는 법칙입니다. 이것은 전기장이 역학적 에너지가 보존되는 보존장(conservative vector field)이기 때문입니다. (물론 전기장이 시간에 따라서 변하면 보존장이 아니게 되지만, 회로이론 범위 내에서는 이 상황도 quasistatic field으로 보고 KVL을 적용할 수 있어요.)

  사실 주파수가 높아지는 경우에는 다른 분석 기법을 적용해야 하지만, 일반적으로 KCL과 KVL은 모든 직류 회로와 교류 회로를 분석할 때 이용되는 사실상 절대적인 규칙입니다. 다양한 문제를 풀어보면서 이 두 법칙에 익숙해지도록 연습하는 것이 중요합니다.

2.4. 연산증폭기(Op Amp) 살펴보기

  한편으로 연산증폭기(Operational Amplifier, Op Amp)라는 능동소자(active element)가 중간중간 등장합니다. 이것은 반도체로 구현되는 소자로서, 사실 자세한 내부 구조나 동작 원리에 대해서는 전자회로 과목과 반도체소자 과목을 공부한 후에 이해할 수 있습니다. 이 과목에서는 Op Amp의 입력전압과 출력전압 사이에 어떤 관계가 성립하고, 이를 이용해 어떤 회로를 만들 수 있는지에 대해서만 다룹니다.

그림 3. 연산증폭기 기호.

  Op Amp의 모양은 위 그림과 같습니다. 두 개의 입력전압을 받아서 하나의 출력전압을 내놓는 식으로 작동합니다. 각각의 입력전압을 $v_{in+}$, $v_{in-}$으로 표기하면 출력전압 $v_{out}$에 대해 $$v_{out}=A(v_{in+}-v_{in-})$$ 의 관계가 성립하므로, Op Amp는 두 입력전압 값에 의존하는 종속전압원입니다. $A$는 보통 100 이상의 큰 양수로 이득(gain)이라고 부릅니다. 입력전압 아래 첨자에 있는 +/- 기호는, 해당하는 입력값이 증가할 때 출력전압이 증가하는지 혹은 감소하는지를 나타내는 것입니다.

  회로에서 Op Amp를 이용하는 방법으로는 여러 가지가 있습니다. 가장 많이 사용하는 방식은 출력이 나오는 부분에 회로를 더 연결해서 $v_{in-}$ 쪽으로 신호가 전달되도록 만드는 것인데, 이를 음성피드백(negative feedback, 부귀환)이라고 부릅니다.

그림 4. 음성피드백(negative feedback, 부귀환) 예시.

  위의 회로가 음성피드백을 사용하는 대표적인 예시입니다. 출력전압이 $v_{out}$으로 걸리게 되면 $R_2$에 $$\frac{v_{out}}{R_1+R_2}$$의 전류가 흐르고, 그에 따라서 $v_{in-}$ 단자 쪽으로는 $$\frac{R_2}{R_1+R_2} v_{out}$$의 전압이 걸리게 됩니다. 앞서 언급한 Op Amp의 입출력 관계를 고려해보면 결국 $$A(v_{in}-\frac{R_2}{R_1+R_2}v_{out})=v_{out},$$ $$v_{out}=\frac{A}{1+(\frac{R_2}{R_1+R_2})A}v_{in}$$ 이라고 정리할 수 있습니다[2].
  Op Amp가 이용되는 회로를 분석할 때, 처음부터 실제 Op Amp의 동작을 일일이 고려하기는 어렵습니다. 그렇기 때문에 “이상적인” Op Amp라는 가정을 가지고 회로를 먼저 파악하게 됩니다. Op Amp가 “이상적”이라는 뜻은 아래와 같습니다:

1. 입력쪽으로는 전류가 들어가지 않고,
2. 출력 단자는 그 쪽에 어떤 회로가 연결되어 있건 설정된 전압을 잘 내놓으며,
   (출력 임피던스가 0이 된다고 하거나, 부하 효과가 없다고도 표현합니다)
3. Op Amp의 gain A는 양의 무한대라고 취급할 수 있습니다.

앞서 예시로 들었던 Op Amp 회로를 고려해보면, $A \rightarrow \infty$이 되어 $$v_{out}=(\frac{R_1+R_2}{R_2})v_{in}=(1+\frac{R_1}{R_2} ) v_{in}$$이 성립하고, $v_{out}=A(v_{in+}-v_{in-})$에서 $v_{out}$이 유한한 값이지만 $A \rightarrow \infty$ 이므로$$v_{in+}=v_{in-}$$이라는 관계가 성립합니다. 따라서 이상적인 Op Amp라는 가정에 기반해서 회로를 분석할 때는, 처음부터 두 입력 전압이 같다고 두고 회로를 분석해나가기도 합니다. 

2.5. Thevenin의 정리와 두 가지 등가회로

  회로가 간단하면 모든 것들을 일일이 분석해도 되지만, 복잡한 회로는 하나하나 다 뜯어보면서 분석해나가기가 어렵습니다. 이 경우에는 회로를 몇 개의 덩어리로 조각내서 “분석해볼 수 있지 않을까?”라고 생각할 수 있는데, 이것을 가능하게 해주는 것이 Thevenin의 정리입니다. 아래에서 같이 살펴보겠습니다.

그림 5. Thevenin의 정리.

  Thevenin의 정리는 바깥으로 두 단자가 튀어나온 선형회로가 있을 때, 이 회로를 단지 저항과 전압원이 두 단자 사이에 직렬 연결된 형태로 이해할 수 있다는 정리입니다. 즉 회로 바깥에서 단자 쪽을 보았을 때, 단자 사이에 연결된 복잡한 회로를 일일이 분석하지 않고 전압원과 저항의 직렬 연결로 간주해도 이 회로의 동작을 충실히 묘사할 수 있습니다. 이렇게 Thevenin의 정리에 따라 주어진 회로의 동작을 똑같이 모사하는 회로를 Thevenin 등가회로라고 불러요.

  저항과 독립전원, 그리고 다른 전압이나 전류에 선형적으로 의존하는 종속전원들로 만들어진 회로는 선형회로입니다. 따라서 직류회로를 분석할 때 Thevenin의 정리를 적용할 수 있어요. 수업 후반부에 다루는 교류회로의 경우는 상황이 조금 복잡하지만, 페이저라는 개념을 도입해 저항을 임피던스로 일반화하면 R, L, C 세 개의 소자 모두 복소수 전압과 복소수 전류 사이에 선형적인 관계가 성립한다고 볼 수 있습니다. 그에 따라 Thevenin 정리처럼 직류 저항회로 분석에 적용할 수 있는 분석 기법들을 교류회로에도 적용할 수 있어요. 여기서는 직류 회로에서의 Thevenin의 정리에 대해서만 다루어보도록 하겠습니다.

그림 6. Thevenin의 정리 예시문제 회로도.

  위 회로의 Thevenin 등가회로를 찾는 문제를 생각해봅니다. 이 회로의 동작을 전압원과 저항의 직렬연결로 나타낼 수 있다는 것을 알기에, 문제는 전압원의 전압, 그리고 저항값을 찾아내는 것입니다. Thevenin 등가회로의 전압 $V_{oc}$는 바깥에 튀어나온 두 단자를 연결하지 않고 개방(open)했을 때 측정되는 전압입니다. 주어진 예시 문제에서는 2Ω 저항에 전류가 흐르지 않는다는 사실을 이용해 $V_{oc}=-24$V가 되는 것을 알 수 있습니다.

  등가회로의 저항 $R_{th}$를 구하려면 가장 먼저 $V_{oc}$를 0으로 만들어야 합니다. 이를 위해서는 선형회로에서 전압과 전류가 결국 독립전원값들의 일차결합으로 나타난다는 성질을 이용해야 합니다. 즉, $V_{oc}$도 결국 원래 회로의 독립전원들의 일차결합으로 얻어지기에, 원래 회로의 독립전원들을 전부 0으로 만들어야 합니다. 독립전압원이 0이 된다는 것은 곧 양단을 단락시켰다는 것과 같고, 독립전류원이 0이 된다는 것은 양단을 개방했다는 것과 같습니다.

그림 7. Thevenin 등가회로의 저항 찾기.

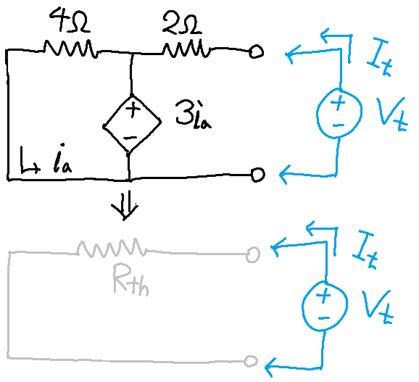
  따라서 오른쪽 그림처럼 독립전원들을 전부 0으로 만들고, 밖으로 나온 단자에 테스트 전압 $V_t$를 걸어 회로로 흘러들어가는 전류 $I_t$로 나누어 $R_{th}$를 구할 수 있습니다. 주어진 문제의 경우, $i_a=0$이 되어 4Ω 양단의 전위차가 발생하지 않기 때문에 $R_{th}=2$Ω이 됩니다. 이를 통해서 주어진 회로의 Thevenin 등가회로를 찾아낼 수 있습니다.

그림 8. 복잡한 회로를 해석하기 위한 Thevenin의 정리의 적용.

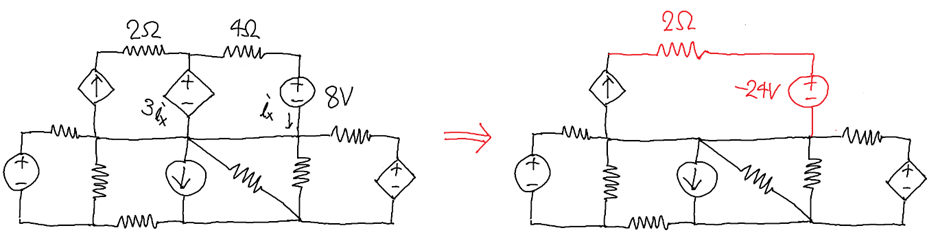
  이제 복잡한 회로가 주어졌을 때, 만약 우리가 일부분의 Thevenin 등가회로를 알고 있다면 위 그림에서와 같이 회로 모양을 조금 더 간단하게 바꿀 수 있습니다. 이렇게 복잡한 상황을 간단히 바꾸어 바라보는 것은 회로 분석의 중요한 철학입니다.

2.6. 에너지 저장 소자(L, C) 회로의 분석

  인덕터(L)는 코일에 전류가 흐르며 만들어지는 자기장에 에너지를 저장하고, 커패시터(C)는 도체 사이 절연체에 형성되는 전기장에 에너지를 저장합니다. 그래서 이 두 소자를 에너지 저장 소자라고 불러요. 저항과 함께 이러한 소자가 사용되면 전압과 전류 사이 관계에 시간에 대한 미분이 추가되므로, 이 회로를 분석하는 문제는 이제 상미분방정식으로 구성된 초깃값 문제(initial value problem)로 바뀌게 됩니다. 특히 에너지 저장 소자가 하나 사용될 때마다 시간에 대한 도함수가 하나씩 증가하는 것이라고 생각한다면, RL 회로나 RC 회로는 에너지 저장소자가 하나만 사용되고 있으므로 1계 미분방정식(first-order differential equation)으로 기술되는 문제가 됩니다.

그림 9. RC 1차 회로.

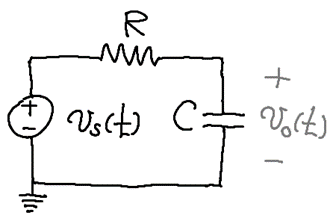
  이 과목에서는 소자의 R, L, C 값이 시간에 따라 변하는 경우를 다루지는 않으므로, 풀어야 하는 미분방정식들은 상수계수 선형미분방정식(constant coefficient linear differential equation)입니다. 위와 같은 RC 회로를 생각해볼게요. 커패시터에 인가되는 전압을 $v_o(t)$라고 하면, R과 C에 흐르는 전류가 똑같으므로 $$\frac{v_s(t)-v_o(t)}{R}=C \frac{dv_o(t)}{dt}$$라고 쓸 수 있습니다. 따라서 위 식을 정리하면 $$\frac{dv_o(t)}{dt}+\frac{1}{RC} v_o(t)=\frac{1}{RC} v_s(t)$$라는 상수계수 선형미분방정식을 얻을 수 있어요.

  이러한 방정식의 해(solution)는 homogeneous solution과 particular solution으로 각각 나누어 구할 수 있습니다. Homogeneous solution은 방정식에서 $v_s (t)=0$인 경우의 해를 의미합니다. 즉,$$\frac{dv_{o,h}(t)}{dt}+\frac{1}{RC} v_{o,h}(t)=0$$이므로, 이 방정식의 해 $v_{o,h}(t)$는 $$v_{o,h}(t)=A \exp(-\frac{1}{RC}t)$$로 구할 수 있습니다. (여기서 $A$는 미정계수로서, 초기조건(initial condition)으로 정할 수 있어요.) 여담이지만, 대부분의 경우 회로는 stable system으로서, homogeneous solution은 시간이 지남에 따라 진폭이 줄어듭니다. 따라서 회로가 작동을 시작한 후 잠시동안만 회로 응답에 나타나기에 회로이론에서는 이를 과도응답(transient response)이라고도 불러요. 

  한편, particular solution은 주어진 $v_s(t)$에 대해서 나타나는 방정식의 해를 의미합니다. $v_s (t)$는 결국에 회로에 가해지는 전원에 대응되므로, 이 $v_s (t)$를 입력으로 생각하면 particular solution은 그에 따른 출력이라고 생각할 수 있어요. 대부분 $v_s (t)$는 직류전압으로서 상수값을 갖거나 일정한 주파수를 갖고 진동하는 사인파 교류전압이며, 그에 따른 particular solution 또한 상수함수 혹은 사인파로 나타납니다. 따라서 이를 정상상태응답(steady-state response)이라고도 부르는데, 특히 사인파 입력전압에 대한 정상상태응답은 과목 후반부에서 공부할 주요 학습목표입니다.

  여기서는 간단하게 $v_s (t)=V_s$라는 직류전압이 회로에 주어진다고 해보겠습니다. 이것은 축전기 양단에 $V_s$라는 일정한 전압을 걸어 축전기를 충전하는 상황에 대응됩니다. 따라서 축전기는 점점 충전되다가 궁극적으로는 양단에 일정한 전압이 나타날 것이라고 생각할 수 있습니다. 즉,$$\frac{dv_{o,p}(t)}{dt}+\frac{1}{RC}v_{o,p} (t)=\frac{1}{RC} V_s$$에서 첫번째 미분항이 0이 되기에, $v_{o,p} (t)=V_{s}$라고 할 수 있어요.

  회로의 완전한 응답(complete response)은 과도응답과 정상상태응답을 합쳐진 형태입니다. 즉,$$v_o (t)=A \exp⁡(-\frac{1}{RC} t)+V_s$$와 같으며, 언급했듯이 미정계수는 초기조건을 이용해서 찾을 수 있어요. 여기서는 만약 축전기가 충전되지 않았다는 조건이 걸려 있었다면 $v_o (t=0)=0$이 되므로,$$v_o (t=0)=A+V_s=0$$로부터 $A=-V_s$라고 할 수 있겠습니다.

  인덕터가 사용된 회로에서도 마찬가지로 인덕터의 전압-전류 관계와 KCL, KVL을 이용해 회로의 응답을 묘사하는 미분방정식을 찾을 수 있습니다. 이 미분방정식의 과도응답과 정상상태응답을 찾은 후에, 둘을 합한 뒤 초기조건을 고려해주면 회로의 완전한 응답을 찾아낼 수 있어요.

  에너지 저장 소자가 2개 사용되면 대부분 2계 미분방정식(second-order differential equation)을 풀어 완전한 응답을 찾아내야 합니다. 전체적인 과정은 똑같지만, 풀어보면 RC, RL 1차회로에 비해 더욱 다양한 형태의 응답을 확인할 수 있습니다.

2.7. 회로의 정현파 정상상태 분석

  일정한 주파수의 사인파 교류 전압으로 전원이 가해진다면, 회로의 응답은 궁극적으로 입력과 동일한 주파수의 사인파로 나타납니다. 이를 정현파 정상상태(사인파의 다른 이름은 정현파입니다)라고 부르며, 정현파 정상상태를 분석할 때는 미분방정식을 푸는 것과는 다른, 어쩌면 더욱 쉬운 방법을 적용할 수 있어요. 한번 차근차근 살펴봅시다.

  Euler의 항등식에 따르면, $$e^{i\theta}=\cos⁡{\theta}+i\sin{\theta}$$라는 관계가 성립합니다. 즉, 사인함수를 생각할 때, 이를 복소수 지수를 갖는 지수함수(complex exponential function)로 생각할 수 있다는 것입니다. 이러한 관점이 어떤 장점을 갖고 있을까요? 얼핏 보면 사인함수 자체로 바라보면 상황이 간단해질 것을, 굳이 복소수로 넘어갔다가 실수로 다시 돌아가는 것 같아 번거롭기도 합니다. 하지만 두 각을 합쳐야 하는 등의 상황에서 복소지수함수는 기존의 삼각함수에 비해 압도적인 계산상의 편리함을 제공합니다. 가령 $\cos⁡(\alpha+\beta)$를 계산해야 한다고 생각해봅시다. 지수함수로 생각해보면 $$e^{i(\alpha+\beta)} =e^{i\alpha} e^{i\beta}$$이 성립하며, $$e^{i(\alpha+\beta)} = \cos⁡(\alpha+\beta)+i\sin ⁡(\alpha+\beta),$$ $$\begin{align*} e^{i\alpha} e^{i\beta}&=(\cos⁡{\alpha}+i \sin{⁡\alpha} )(\cos{\beta}+i \sin{⁡\beta} )\\ &=( \cos⁡{\alpha} \cos⁡{\beta}-\sin{⁡\alpha}\sin{⁡\beta} )+i(\sin{⁡\alpha} \cos{⁡\beta}+\cos{⁡\alpha} \sin{\beta}) \end{align*}$$이므로, $$\cos⁡(\alpha+\beta)=\cos⁡{\alpha}\cos{\beta}-\sin{⁡\alpha}\sin{⁡\beta},$$ $$\sin⁡(\alpha+\beta)=\sin{⁡\alpha} \cos{⁡\beta}+\cos{⁡\alpha} \sin{\beta}$$이라는 것을 알 수 있습니다. 사실 이것은 결국 삼각함수의 덧셈정리 공식이기는 합니다. 하지만 $ \cos⁡(\alpha+\beta)$를 계산하기 위해 이전까지는 공식을 잘 기억한 뒤 각도를 하나하나 대입해서 풀어야 했다면, 복소지수함수를 도입한 이후부터는 단지 두 복소수를 잘 곱하기만 하면 됩니다. 그렇기에 복소지수함수가 삼각함수를 다루기 더 쉽게 해준다고 짐작할 수 있을 거예요.

  이를 이용하면 사인파 교류회로를 더욱 쉽게 분석할 수 있습니다. 구체적으로 표현해보면, 미분방정식을 풀기 위해 더 이상 미분을 하지 않아도 됩니다. RLC 직류회로를 분석하는 문제를 통해 이 복소수 접근법을 좀더 자세히 살펴봅시다.

그림 10. RLC 직렬 공진회로.

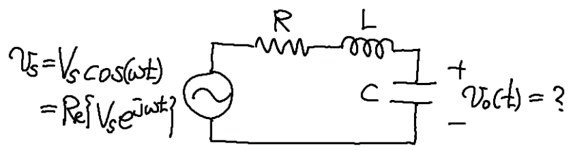
  위 그림처럼 전압원이 RLC 직렬회로에 $v_s (t)=V_s \cos{⁡\omega t}$ $(V_s>0)$의 전압을 인가할 때, 축전기에 걸리는 전압 $v_o (t)$를 구해봅시다. 만약 이전처럼 미분방정식으로 문제를 푼다고 하면, 위 회로는$$LC \frac{d^2 v_o}{dt^2}+RC \frac{dv_o}{dt}+v_o (t)=v_s (t)$$라는 미분방정식으로 작동을 묘사할 수 있으며, 정상상태는 $v_s (t)=V_s  \cos⁡ωt$인 경우의 particular solution임을 이용해서 문제를 풀어야 합니다.

  이제 우리가 하려고 하는 일은 이 정상상태, 혹은 particular solution을 미분방정식을 미분 없이 풀어내는 일입니다. 가장 먼저 해야 하는 일은, $v_s (t)=V_s  \cos⁡ωt$을 $V_s e^{jωt}$의 실수부라고 생각하는 것입니다. 그러면 방정식을 $$LC \frac{d^2 v_o}{dt^2}+RC\frac{dv_o}{dt}+v_o (t)=Re\{V_s e^{jωt} \}$$으로 볼 수 있습니다. 그런데 만약 $v_s (t)$이 $V_s  \cos⁡ωt$가 아닌 $V_s e^{jωt}$인 경우의 방정식의 해를 $\tilde{v}_o (t)$라고 한다면, $$LC \frac{d^2 \tilde{v}_o}{dt^2}+RC \frac{d \tilde{v}_o}{dt}+ \tilde{v}_o (t)=V_s e^{jωt}$$이 성립하므로, 양변의 실수부만 읽어보면 $$ \begin{align*} LC \frac{d^2}{dt^2} Re\{ \tilde{v}_o (t)\}+RC \frac{d}{dt} Re\{ \tilde{v}_o (t)\}+Re\{ \tilde{v}_o (t)\} \\ =Re\{LC \frac{d^2 \tilde{v}_o (t)}{dt^2}+RC \frac{ \tilde{v}_o (t)}{dt}+ \tilde{v}_o (t)\}=Re\{V_s e^{jωt} \} \end{align*} $$ 이 성립합니다. 따라서 $v_s (t)=V_s e^{jωt}$인 경우 방정식의 해 $\tilde{v}_o (t)$를 찾아낸다면, $\tilde{v}_o (t)$의 실수부가 입력 $V_s \cos⁡ωt$에 대한 회로의 응답 $v_o (t)$이 된다고 말할 수 있을 것입니다.

  한편, 선형미분방정식으로 기술되는 LTI 시스템에서는 $x(t)=e^{st}$라는 입력이 시스템에 들어가면 그에 대한 출력이 $y(t)=H(s) e^{st}$꼴의 형태로 나오게 됩니다. 이것을 회로이론의 언어로 바꾸어보자면, 입력 $v_s (t)$가 $e^{jωt}$에 상수가 곱해진 형태로 주어질 때(즉, $s=jω$로 대입한 것입니다), 그에 대한 회로의 응답도 $e^{jωt}$에 어떤 계수가 곱해진 형태로 나타나며, 이 계수는 주파수 $ω$에 따라서 결정된다는 의미입니다. 그 이유나 구체적인 조건에 대해서는 3학년 과목인 신호 및 시스템에서 배우며[3], 여기에서는 결과만 이용해 보도록 하겠습니다.

  언급한 내용을 숙지하고 있으면 결국 $\tilde{v}_o (t)=\tilde{V}_o (s) e^{st}=\tilde{V}_o (jω) e^{jωt}$라는 형태로 나타날 것임을 알 수 있습니다. 이 $\tilde{V}_o (jω)$가 어떻게 생겼는지는 $e^{jωt}$를 시간에 따라서 미분하면 단지 앞에 $jω$가 곱해진다는 사실을 이용하면 알 수 있습니다. 방정식의 $\tilde{V}_o (t)$ 자리에 $\tilde{V}_o (jω) e^{jωt}$를 대입하면$$((jω)^2 LC+jωRC+1)\tilde{V}_o(jω) e^{jωt}=(1-ω^2 LC+jωRC)\tilde{V}_o (jω) e^{jωt}=V_s e^{jωt}$$이 되므로, $\tilde{V}_o (jω)$는 $$\tilde{V}_o(jω)=\frac{V_s}{1-ω^2 LC+jωRC}$$이 됩니다. 따라서, 복소수 $\tilde{V}_o (jω)$의 절댓값(modulus)과 편각(argument)을 각각 $$|\tilde{V}_o (jω)|=\frac{V_s}{\sqrt{(1-ω^2 LC)^2+(ωRC)^2}},$$ $$\phi=-\arctan⁡(\frac{ωRC}{1-ω^2 LC})$$ 라고 할 때, $\tilde{v}_o (t)=| \tilde{V}_o (jω)| \exp⁡(j(ωt+ϕ))$이므로, 회로의 정현파 정상상태 응답은 $$v_o (t)=Re\{\tilde{v}_o (t)\}=|\tilde{V}_o (jω)| \cos⁡(ωt+ϕ)$$라고 풀어낼 수 있게 됩니다.

  위의 풀이를 살펴보면, 축전기의 전압을 구하는 문제는 결국 복소수 $\tilde{V}_o (jω)$를 찾아내는 문제로 귀결되는 것을 알 수 있습니다. 즉 복소수와 축전기 전압은 일대일 대응 관계에 있어, 복소수의 절댓값과 편각을 알면 바로 전압의 진폭과 위상을 찾을 수 있습니다. 이처럼 교류 신호의 진폭과 위상 정보를 담고 있는 복소수를 페이저(phasor)라고 부릅니다. 이 예제에서는 전압을 찾기 위해 페이저를 이용했지만, 전류를 찾는 경우도 마찬가지로 페이저를 이용할 수 있습니다.

  한편, 페이저는 L과 C의 전압과 전류 사이의 관계를 저항처럼 취급할 수 있게 해줍니다. 전원이 $ω$라는 주파수의 사인파 형태로 들어오므로 이것을 $e^{jωt}$ 모양으로 나타낸다고 할 때, L의 전압과 전류는 각각 $\tilde{V}_L e^{jωt}$와 $\tilde{I}_L e^{jωt}$로, C의 전압과 전류는 각각 $\tilde{V}_C e^{jωt}$와 $\tilde{I}_C e^{jωt}$로 나타날 것입니다. 이제 미분으로 기술되는 L과 C의 전압과 전류 관계를 고려해보면 $$\tilde{V}_L e^{jωt}=L \frac{d}{dt} \{\tilde{I}_L e^{jωt} \}=jωL\tilde{I}_L e^{jωt},$$ $$\tilde{I}_C e^{jωt}=C \frac{d}{dt} \{\tilde{V}_C e^{jωt} \}=jωC\tilde{V}_C e^{jωt}$$가 됩니다. 따라서 L과 C의 전압 페이저와 전류 페이저 사이의 비율은 각각 $$\frac{\tilde{V}_L}{\tilde{I}_L} =jωL=Z_L,   \frac{\tilde{V}_C}{\tilde{I}_C} =\frac{1}{jωC}=Z_C$$이 되며, 이를 각각 L과 C의 임피던스(impedance)라고 부릅니다. 직류 회로에서 적용하던 저항 개념을 교류회로로 일반화한 것이라고 생각할 수 있습니다.

  이렇게 교류 회로를 임피던스들의 조합으로 이해하면, 이전까지 직류 회로에서 이용했던 여러 분석 기법을 교류회로 분석에도 적용할 수 있습니다. 예를 들어, 앞에서 얻은 RLC 직렬회로에서의 축전기 전압을 임피던스를 이용해 다시 구해보겠습니다. 우선 R, L, C 각각의 임피던스들이 직렬로 연결된 것이므로 이 회로의 전류 페이저는 $$\frac{V_s}{Z_R+Z_L+Z_C}=\frac{V_s}{R+jωL+\frac{1}{jωC}}$$입니다. 따라서 축전기에 걸리는 전압의 페이저는 전류와 임피던스를 곱한 형태인 $$\frac{V_s}{R+jωL+\frac{1}{jωC}}\frac{1}{jωC}=\frac{V_s}{1-ω^2 LC+jωRC}$$ 로, 이는 앞에서 구한 $\tilde{V}_o (jω)$ 식과 똑같은 형태입니다.

3. 선배의 조언

  회로이론은 물리적으로 전기를 다루는 분야를 전공하고자 한다면 필수적으로 알아두어야 하는 과목입니다. 집적회로나 무선공학, 전력공학과 같은 분야에서는 회로이론 내용에 기반하여 직접 회로를 설계하며, 반도체와 전자물리 분야에서는 물리적인 현상을 회로로 모델링하여 이를 분석하는 등의 연구가 이루어집니다. 이 분야로의 진학을 계획하고 있다면 가능한 회로이론에 나오는 내용들을 친숙하게 만드는 것을 추천드립니다.

  그런데 이처럼 과목 내용이 다양한 분야에서 범용적으로 쓰인다는 것은 한편으로는, 과목에서 소개되는 내용들이 후속 과목에서 다시 등장한다는 것을 뜻하기도 합니다. 회로이론을 공부하는 시점에서는 이해가 잘 되지 않거나 와닿지 않더라도, 나중에 가서 이해가 되는 경우가 종종 있는 것 같아요. 저는 회로이론을 공부할 당시 등가회로 개념이나 정현파 정상상태 내용이 막연하게 느껴졌었는데, 등가회로를 도입하는 이유는 나중에 3학년 아날로그전자회로 과목을 공부하면서, 시간에 따른 시스템의 응답을 정현파 정상상태에 대해서만 중점적으로 분석하고 넘어가는 이유는 신호 및 시스템과 3학년 전자기학, 양자역학의 응용 과목에서 이해하게 되었습니다. 그렇다 보니지금 배우는 이론 내용이 이해되지 않는다고 너무 좌절하지 않으셨으면 좋겠습니다. 결국 꾸준한 사람들이 승리를 쟁취하는 것 같아요.

  그리고 공부를 하면서는 가능한 다양한 문제를 풀어보고, 혹여 답지를 보더라도 답지를 그대로 따를 필요는 없다고 말씀드리고 싶습니다. 수학이나 물리 과목은 대부분 정해진 논리가 있지만, 회로는 보는 사람마다 분석하는 과정이 다양합니다. 따라서 답지를 집필한 사람과 분석 관점이 다른 경우가 정말 많은 것 같아요. 누구는 직접 회로 성분을 일일이 풀어갈 수도 있고, 누군가는 등가회로 개념을 이용해 회로를 차곡차곡 정리해가면서 문제를 풀 수도 있습니다. 결국에는 KCL, KVL과 같은 조건들이 회로에 잘 적용되는 답이 맞는 답이기 때문에, 우선 여러 문제를 풀어보며 내가 회로를 잘 분석해낼 수 있는지 확인하고, 다양한 접근법을 시도하면서 문제마다 효율적인 회로 분석 기법을 찾는 연습을 해보는 것이 좋은 회로 공부법이라고 생각합니다.

4. 맺음말

  2학년 봄 학기에 수강하는 기초회로이론 및 실험 과목은 앞으로 전기정보공학부에서 하게 될 공부의 기반을 다져주는 과목입니다. 그러나 한편으로는 이론과 실습 자체가 부담스럽게 다가와 전공 진입으로의 장벽으로 느끼는 친구들도 있는 것 같습니다. 장기적인 시선으로 바라보면 기초회로이론에서 공부하는 내용들은 이후에 수강하는 과목들에 다시 등장하는데, 회로이론에서 다룬 경험이 이러한 과목들을 공부하는 데에 큰 도움을 줍니다. 그렇기에 힘들더라도 무너지지 않고, ‘이제 진정한 전기정보공학부의 일원이 되는구나’ 하는 느낌으로 꾸준히 해나가보면 좋겠습니다. 내용도 한번 쭉 정리해보고, 문제도 다양하게 풀다 보면 회로를 보는 눈이 모르는 사이에 어느 순간 갑자기 성장해 있을 거예요. 그리고 여러분들께서 진정 공부를 해나갈 전공분야를 정할 때, 기초회로이론 및 실험에서 익힌 지식과 경험이 도움이 되길 바랍니다. 진정한 전기정보공학도가 된 여러분을 진심으로 환영합니다!

References

[1] Dorf, R. C. & Svoboda, J. A., Introduction to Electric Circuits. 5th ed. Wiley (2018). 
[2] Razavi, B., Fundamentals of Microelectronics. 3rd ed. Wiley (2021).
[3] Oppenheim, A. V., Willsky, A. S. & Nawab, S. H., Signals and Systems. 2nd ed. Pearson (2015).