에너지자원공학과: 신재생에너지

석유 시대가 끝난다는 이야기를 한 번쯤 들어보셨을 겁니다. 언젠가 고갈될 석유를 대체할 수 있는 수단은 무엇이 있을까요? 신재생 에너지 강좌를 소개합니다.

1. 과목에서 배울 수 있는 내용

1.1 과목의 전반적인 개요

여러분은 신재생에너지 라는 단어를 들으면 태양광이나 풍력, 지열 등의 재생에너지가 바로 떠오르실 텐데요, 신재생에너지는 여기에 기존 화석연료를 응용한 신에너지를 융합한 단어입니다.

에너지자원공학과 3학년 1학기 전공선택 과목인 신재생에너지에서는 신에너지와 재생에너지를 모두 다루며, SAM 프로그래밍과 아두이노를 활용한 실습과 함께 전반적인 신재생에너지를 배울 수 있습니다.

1.2 키워드 별 개념 설명

신재생에너지는 신에너지와 재생에너지를 합한 것으로, 화석연료를 대체하는 수력, 풍력, 태양열과 같은 무공해의 재생 가능한 자연 에너지입니다. 무공해, 무한정이면서 다양한 자연 에너지의 특성과 기술을 활용하여 석탄, 석유, 천연가스 등 화석연료와 원자력을 사용하는 기존 에너지를 대체하는 재생 가능한 에너지로, 신재생에너지 수업에서 다루는 태양광, 태양열, 풍력 수력 등 외에도 수소에너지나 연료전지, 석탄 가스화 에너지 등이 있습니다.

우리나라는 현재 탄소배출량을 2050년까지 0으로 만드는 Net Zero 정책을 목표로 하고 있고, 이를 위해 RE 100을 통한 기업들의 100% 신재생에너지 전환이나 CF 100 정책을 시행 중입니다. 환경 정책의 중요성이 매우 커진 요즘, 신재생에너지 수업에서는 기존 신재생 에너지를 분석하는 방법 및 연구가 진행되는 방법을 배울 수 있습니다.

1. 태양열 발전

가장 먼저 신재생에너지의 대표주자인 태양열 발전에 대해 배우게 됩니다. 태양열의 절반 가량이 반사되거나 대기에 흡수되고, 지구에 도달한 태양에너지는 지구 전체 표면에 골고루 분포한다는 가정 하에 지구 전체 표면에서의 평균 일사량은 Stefan-Boltzmann law에 의해 약 $165W/m^2$ 입니다.

$$Total\, Emission(L)=\sigma \epsilon AT_s^4\\(\sigma: Stefan-Boltzmann\, constant=5.67\times10^{-8}W/m^2K^4, T_s: 6000K) \\ Solar\, Irradiance(I)= \frac{L}{A}=\frac{L_s}{4\pi R_d^2}\simeq1367W/m^2\\(R_d:태양과\,지구\,사이\,거리=1.49\times10^8km) \\ \therefore Total\,Sun\,Power\,on\,Earth=I\times A=I\times \pi R_E^2\simeq173000TW\\(R_E:\, 지구\, 반지름=6371km) \\ \& \,Average\, Sun\, Power\, on\, Earth=\frac{0.5P}{A}=\frac{0.5P}{4\pi R_E^2}\simeq168W/m^2$$

그림 1-3. 지구에의 태양 일사량과 일률, 평균 일사량

사람 한 명이 1년간 생활하는 데 필요한 에너지를 대략 $1.184\times 10^{21} J$로 계산합니다. 이로부터 모든 태양열 에너지를 15% 효율로 전기에너지로 전환할 수 있다면, 현재 인구수를 상회하는 $1.46\times 10^{10}$명을 부양할 수 있습니다. 이처럼 반영구적이고 풍부한 태양열 에너지를 효율적으로 사용하기 위해, concentration ratio의 도입으로 태양열 집열판의 효율을 높이는 방법을 배우게 됩니다.

Concentration Ratio $C$는 absorber 면적에 대한 전체 노출 면적, $C=\frac{A_o}{A_{ab}}$로 정의됩니다. 예를 들어, 평판형 포물면 집열기는 $C=\frac{WL}{2\pi RL}=\frac{W}{2\pi R}$로 계산할 수 있습니다. 태양의 고도에 따라 태양광의 입사각이 바뀌고 태양광이 absorber에 다다르지 못하게 만들기 때문에, 태양광이 absorber에 도달할 수 있는 최대 입사각인 $\theta_a$ 를 계산해야 합니다.

그림 4. 평판형 포물면 집열기의 개요도

$C$와 $\theta_a$의 관계를 알아보기 위해 삼차원 구체형 태양열 집열판을 생각해 봅시다. 앞서 본 Stefan-Boltzmann law와 융합하면 absorber의 온도 $T_{ab}$를 구할 수 있습니다.

$$I\times A_o=\sigma A_{ab}T_{ab}^4,\;T_{ab}=\left(\frac{A_o}{A_{ab}}\times\frac{I}{\sigma}\right)^{1/4}=\left(\frac{CI}{\sigma}\right)^{1/4}$$
Absorber의 반경 $r$과 노출면의 반경 $d$에 대해 $r\ll d$ 를 가정하면, $sin\theta=r/d$ 로 근사할 수 있습니다. 에너지 보존에 의해 $4\pi r^2 \sigma T_s^4=I\times4\pi d^2$이 성립하므로, $T_{ab}$ 는 다음이 됩니다.
$$T_{ab}^4=\frac{CI}{\sigma}=C\left(\frac{r}{d}\right)^2T_s^4=Csin^2\theta T_s^4$$
마지막으로 열역학 제 2법칙에 의해 $T_{ab}\leq T_s$이고, 등호는 $\theta=\theta_a$일 때 성립합니다. 따라서 $C$와 $\theta_a$사이 관계는 다음과 같습니다.
$$C_{3D}\leq\frac{1}{sin^2\theta_a}$$

그림 5. 삼차원 구형 태양열 발전기

2. 풍력발전

다음으로 우리나라에서도 많은 설치 사례를 볼 수 있는 풍력발전을 다루게 됩니다. 풍속 $U$, 단면적 $A$, 밀도 $\rho$의 유체가 갖는 운동에너지는 다음과 같습니다.
$$P_o=\frac{1}{2}mU^2=\frac{1}{2}(\rho AU)U^2=\frac{1}{2}\rho AU^3=\frac{\pi}{8}\rho D^2U^3\; (직경 =D인\;원형\;터빈\;가정\;시)$$

이때 터빈을 통과하며 운동에너지가 낮아진 유체는 유속이 줄어들며, 이를 간섭계수로 나타냅니다. 이 교란으로 인해 풍력 터빈은 에너지 발전이 줄어들며, 줄어든 에너지는 파워계수로 나타냅니다.

간섭계수(intereference factor) : $a=\frac{U_0-U_1}{U_0}$,
파워계수(power coefficient): $C_p=\frac{P_T}{P_O}$

간섭계수와 파워계수 사이에는 $C_p=4a(1-a)^2$의 관계가 있습니다. 이에 따라 풍력터빈의 효율은 $a=\frac{1}{3}$일 때 극대값을 갖습니다.

파워계수를 계산할 때는 흔히 날개끝 속도비 $\lambda$를 사용합니다. 풍력터빈의 날개가 많을수록 바람과 상호작용이 커져 에너지를 많이 얻을 수 있지만 효율이 낮아지게 됩니다. 따라서 날개끝 속도비 $\lambda$에 따른 파워계수는 극대값을 갖는 형태가 됩니다. 이러한 극대값을 Betz 한계라고 합니다.

그림 6. 날개끝 속도비에 따른 파워계수 그래프

3. SAM 프로그래밍 및 아두이노 실습

이론수업 내용이 끝나고 나면, SAM 프로그램을 이용한 분석과 아두이노, 앱인벤터를 통한 실습을 진행하게 됩니다.

SAM(System Advisor Model)은 미국 신재생에너지 연구소 National Renewable Energy Laboratory, NREL)에서 개발한 시뮬레이션 프로그램입니다. 지리정보시스템에 등록된 위성사진을 이용하여 원하는 지역에 발전 설비를 설치했을 때, 모델링을 통해 발전량/elevation/그림자 비율 등 다양한 값을 계산할 수 있습니다.

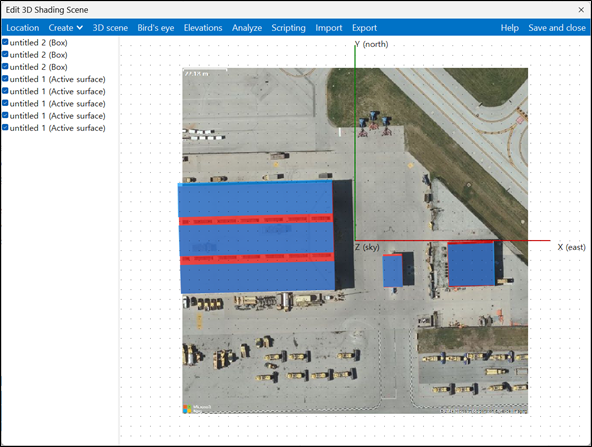
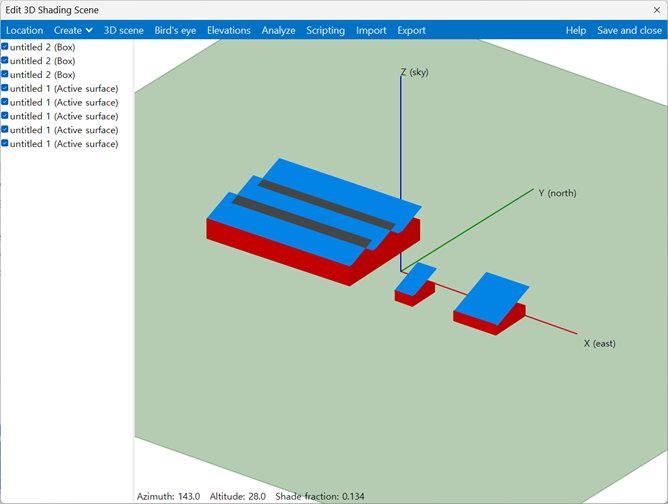
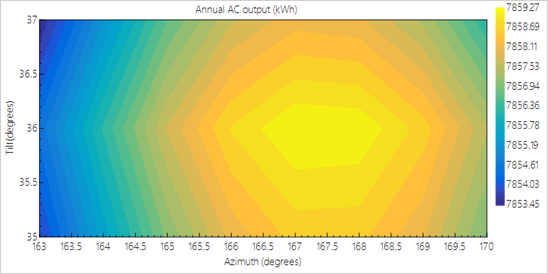
그림 7-9. SAM 프로그램을 이용해 Chicago O’Hare Airport 인근에 태양광 발전기 설치 시, 설치 각도에 따른 발전량 분석을 진행한 모습

2. 선배의 조언

신재생에너지는 에너지자원공학과의 다른 전공수업과는 다르게 교양의 성격이 강한 수업입니다. 이에 따라 수업의 전 후로 필요한 수강과목은 없으며, 기본 수학/물리 지식이 있다면 수업 내용을 어렵지 않게 이해할 수 있습니다.

SAM프로그래밍, 아두이노, 앱인벤터 등 실습의 비중이 수업의 절반 정도를 차지하는 만큼 딱딱한 이론수업을 벗어나 다양한 실험을 부담없이 진행할 수 있는 수업입니다. 만약 SAM프로그래밍 분야에 관심이 있는 분이라면, 2학년 2학기 전공 선택 과목인 에너지 GIS과목을 수강하시는 것 또한 추천합니다.

3. 진로 선택에 도움되는 점

신재생에너지는 차세대 에너지원의 전반적인 내용을 넓게 다루는 수업입니다. 따라서 차세대 에너지에 관심이 있는 분들은 필수적으로 익혀 둬야 하는 과목일 것입니다.

또한 이론적인 내용보단 실습의 비중이 높은 과목입니다. 프로그램을 이용해 프로젝트를 수행하고, 입지 분석을 실시하는 데 관심이 있는 분들께는 적극 추천하는 수업입니다.

4. 맺음말

다양한 실습 외에도, 소형 LED나 태양열 발전기 키트 등을 교구로 만날 수 있어 수업에 몰입하기 좋은 수업입니다. 신재생에너지와 시뮬레이션에 관심이 있으신 분들이라면, 다양한 수업 자료들을 참고하시어 즐거운 수강 되시길 바라겠습니다.

출처: 윤영수, 손정민, 하태준, 차왕석, 박용준, [신재생에너지], 동화기술(2015)