안녕하세요? 저는 공우 11.5기 최원혁이라고 합니다.
이 글에서는 저와 함께 제어와 경험적 모델링에 대해 간단하게! 알아봅시다!
모델링이 뭐지?
이 글에 들어오신 분들은 '모델링이 무엇인지?'에 대해 다양한 생각을 가지고 계실 것 같습니다. 전공에서 모델링이라는 걸 다뤄본 분들도 계실 거고, 아예 처음 보시는 분들도 계실 텐데요, 사실 분야마다 이 '모델링’이라는 용어가 상당히 다양한 용어로 사용되고 있습니다.
오늘 저와 함께 알아볼 모델링은 정확히 말하면 '동적 모델링’입니다. 어떤 시스템에서, 입력이 변화할 때 출력이 시간에 따라 어떻게 변화하는지 그 관계를 파악하는 것을 의미합니다.
…이렇게 얘기하니까 이해가 안 되고 조금 어렵죠? 그래서 이번 글에서는 이해를 돕기 위해서 일상생활과도 연관된 '샤워기’를 예시로 들어서 설명해보려고 합니다.

샤워할 때, 적당하게 따뜻한 물 온도를 맞추기 위해 고생한 경험 한 번씩은 있으셨을 거라 생각합니다. 게다가 옆에 들어온 사람이(아니면 윗집이) 변기 물을 내리거나 물을 많이 쓰면 갑자기 온도가 내려가서 짜증났던 경험도 있으셨을 겁니다. 내가 수도꼭지를 얼마큼 돌리면 물 온도는 어떻게 변할지? 그걸 알면 훨씬 맞추기가 쉬울 텐데요…
그래서 그걸 알아보는 과정이 바로! 모델링입니다.
그럼 이제 계산해보면 되니까 다 해결된 거 아닐까요? 안타깝지만 문제가 남아 있습니다. 혹시 샤워기 내부 구조를 알고 계신가요?

이렇게 복잡한 내부구조에다가, 유체역학이나 열역학을 열심히 적용해서 물 온도를 계산해보는 게 과연 가능할까요?

사실 이런 복잡한 구조에서 저런 방정식을 푼다는 건 불가능에 가깝고, 어떻게 푼다고 하더라도 너무 해가 복잡해서 저걸 물 온도 맞추는 데에 실시간으로 계산해서 써먹기에는 어려울 겁니다.
지금까지 우리가 시도한 게 바로 이론적 모델링입니다. 계의 구조를 파악하고, 구성방정식을 세우고 풀어서 모델을 얻는 방법이죠. 풀 수만 있다면, 상당히 근사한 답을 얻을 수 있습니다!
…풀 수만 있다면요. 풀기가 너무 어렵고, 복잡한데다가 실시간으로 계산해서 써먹기에는 불편한 점이 많습니다.
이 대안으로 등장한 것이 바로 경험적 모델링입니다. 경험적 모델링은 이런 구조에 대한 이해, 보존 법칙과 같은 과학적 원리 없이 실험해서 모은 데이터만으로 모델을 얻는 방법입니다. 이런 방법은 아주 쉽고, 계산도 간단하고, 얻은 해를 써먹기도 쉽습니다!
당연히 조금 오차가 있겠지만, 공학도로서 이 정도 오차는 무시해도 되겠죠.

이런 거 몰라도 샤워 잘 했는데
그런데 모델링은 왜 해야 할까요? 사실 조금 이상함을 느끼셨을 수도 있습니다. 왜냐하면 여러분들은 모델링이 뭔지 모르고도 적어도 십 년 이상을 적당히 물 온도 맞추면서 샤워를 해오셨기 때문입니다! 어떻게 된 걸까요?
여러분들이 지금까지 물 온도를 맞춰온 방식은 사실 단순합니다. 물을 맞아 봐서 차가우면, 수도꼭지를 뜨거운 쪽으로 조금 돌리고, 물이 뜨거우면, 차가운 쪽으로 조금 돌립니다. 이러한 방식을 피드백 제어라고 부릅니다. 직접 결과를 본 후에 피드백한다는 의미죠. 이런 방식의 장점은 이미 아시겠지만, 원리를 전혀 모르더라도 제어가 잘 된다는 점입니다!

그러면 모델링이 왜 필요할지 정말로 의문이 가실 수도 있습니다. 그런데 상상해봅시다. 옆 사람이 갑자기 변기 물을 내려서 물이 갑자기 차가워졌습니다. 피드백 제어에 따르면 여러분은 수도꼭지를 뜨거운 쪽으로 돌려서 물 온도를 다시 맞춥니다. 하지만 조금 시간이 지나면 너무 뜨거워져서 다시 차가운 쪽으로 돌려야 하고, 결국 수도꼭지를 이리저리 돌리는 지루한 핑퐁을 다시 시작해야만 합니다.
여러분이 모델링을 통해서 모델을 잘 알고 있다면, 변기 물이 들리는 순간 수도꼭지를 잘 조절해서 계속해서 따뜻한 물을 맞도록 할 수도 있습니다. 이런 방식을 결과를 보기 전에 미리 조절한다고 해서 피드포워드 제어라고 부릅니다. 이렇게 하려면 아무래도 모델링이 필요하겠죠?
그럼 그 모델링이라는 거, 한 번 해볼까요?
그렇다면 이제 경험적 모델링을 해봅시다! 우리에겐 이제 결정해야 할 상황이 크게 두 가지가 있습니다.
- 어떤 실험을 할까?
- 어떤 모델을 골라서 fitting할까?
차근차근 살펴보도록 합시다.
어떤 실험을 할까?
어떤 실험을 할지는, 정말 다양한 선택지가 있지만, 가장 기본적인 세 가지를 알아보도록 합시다.
첫째는, Step Change입니다.

위처럼, 어느 한 순간에 불연속적으로 값을 변화시키는 방법을 Step Change라고 합니다. 참고로 input이 0인 건 진짜로 0인 게 아니라, 이전의 값을 다 빼준 거라고 생각하시면 됩니다. (예를 들면 30도에서 35도로 갑자기 바꾼 것은, 0에서 5로 바뀌었다고 표시)
라플라스 변환을 아시거나, 배웠더라도 기억하시는 분이 많을지 모르겠지만, Step Change의 경우 라플라스 변환을 했을 때 정말 깔끔하고 단순한 식을 얻을 수 있습니다.
$$ \mathcal{L}(u(t)) = \int_{0}^{\infty} e^{-st}u(t)dt = M\int_{0}^{\infty}e^{-st}dt = \frac{M}{s} $$
이게 왜 좋은 특성일까…? 나중에 알아보도록 하자.
식 자체로도 단순하고 이런 좋은 특성도 가지고 있어서 가장 많이 이용되는 input이고, 이 글에서도 이것을 기준으로 설명하도록 하겠습니다. 하지만 다른 것도 알아보기는 해야 겠죠?
두번째는 Pulse Input입니다.

이것은 주로 Step Change을 사용하기 어려운 경우에 사용됩니다. 왜 어려울까요? 예를 들어 여러분이 샤워기를 모델링하기 위해 실험을 한다고 해봅시다. 이제 Step Change를 하기 위해서 수도꼭지를 뜨거운 쪽으로 돌린다음, 물을 맞으며 기다립니다!
결과는… 화상을 입겠죠! 이렇게 Step Change를 할 경우 안전 문제가 발생하거나, 제품의 품질 문제가 발생하는 경우에는 Pulse Input을 사용합니다. Pulse는 짧은 시간만 변화시켜도 데이터를 얻을 수 있고, 마지막에는 원래대로 돌아온다는 장점이 있습니다.
세번째는 PRBS(Pseudo Random Binary Sequence)입니다.

PRBS는 이름은 매우 어렵지만, 사실 별 거 없습니다. 그 실체는 -M과 M 사이를 계속해서 왔다갔다하는 input입니다. 왜 이렇게 복잡한 input을 사용할까요? 일단은 평균이 0이기 때문에 우리가 원하는 값에서 크게 벗어나지 않습니다. 또 Random으로 진폭이 큰 값을 사용하면, noisy한 시스템을 다룰 때 오차를 최소화할 수 있다는 장점도 있습니다. 다만 앞에 Pseudo가 붙는 이유는, 실험을 재현하기 위해 의사 난수를 사용하기 때문입니다.
어떤 모델을 고를까?
어쨌든 우리는 Step Change를 이용해 실험을 해서, 온도 변화를 얻었습니다!

이제 이걸 어떤 식에 fitting하면 좋을지를 정해야 합니다. 이런 모델은 크게 Linear Model과 Nonlinear Model로 나눌 수 있습니다.
Linear Model(선형 모델)에 대해 잠깐 알아봅시다. 만약 우리가 모델링 하려는 시스템이 선형 미분방정식을 따른다면, 라플라스 변환을 통해 쉽게 풀수 있습니다.

아마도 우리 시스템이 선형을 띠지는 않겠지만, 선형으로 근사해볼 수 있지 않을까? 이게 바로 핵심 아이디어입니다. 선형으로 근사할 수 있다면 계산하기도 훨씬 쉬우니까요. 이 때문에 Step Change에서 라플라스 변환이 단순한 점이 큰 이점이 됩니다. 해를 구하기가 더욱 쉽게 되죠?
가장 단순한 경우는 1차 모델입니다. 아래처럼 아주 단순한 지수함수 형태를 따른다고 가정하고 데이터를 fitting하는 거죠.

그런데 사실, 이 모델은 너무 단순해서 잘 맞는 일이 거의 없습니다. 만약 실제로는 맞는 경우라고 해도 측정 오차(noise) 때문에 잘 맞아 보이지도 않습니다.
여기서 조금 더 나아가면, FOPTD(First Order Plus Time Delay) 모델을 사용할 수도 있습니다. 이 모델은 위와 똑같이 1차 모델이지만, 변화가 시작되기까지 시간 지연이 있습니다.

조금 더 현실적이죠? 게다가 고차 모델의 경우, 이런 FOPTD 모델로 근사되는 경우가 많다는 것이 알려져 있습니다.
그래도 이 정도로는 충분치 않습니다! 그래서 보통 사용되는 것은 다음과 같은 2차 모델입니다.

이러한 2차 모델은 값이 진동하는 경우도 다 표현할 수 있어서 1차 모델에 비해 훨씬 잘 맞습니다. 여기서도 시간 지연을 추가해서 SOPTD(Second Order Plus Time Delay) 모델을 사용할 수도 있죠!
하지만 슬프게도 세상이 선형 모델에 모두 잘 맞을 수는 없습니다. 전통적으로 비선형적 모델은 데이터를 관찰하고, 대략 비슷한 꼴을 띄는 함수를 찾아낸 후에 nonlinear regression 등을 이용해서 파라미터를 찾는 방식을 사용했습니다. 하지만 이런 방식은 결국 사람이 보고 함수 꼴을 상상해야 한다는 점에서 불확실합니다. 최근에는 이런 파라미터를 사용하지 않는 non parametric 방식을 주로 사용하는데, 대표적으로는 Neural Network가 있습니다.

자세하게는 설명하지 않겠지만, 이 방식은 작은 계산기들(그림 속 동그라미, neuron)을 잘 모은 후에 정답인 input과 output 세트를 많이 준비해서 학습 시키며 답을 얻는 방식입니다. 사람이 직접 식을 세우는 게 아니기 때문에 조금 더 객관적입니다.
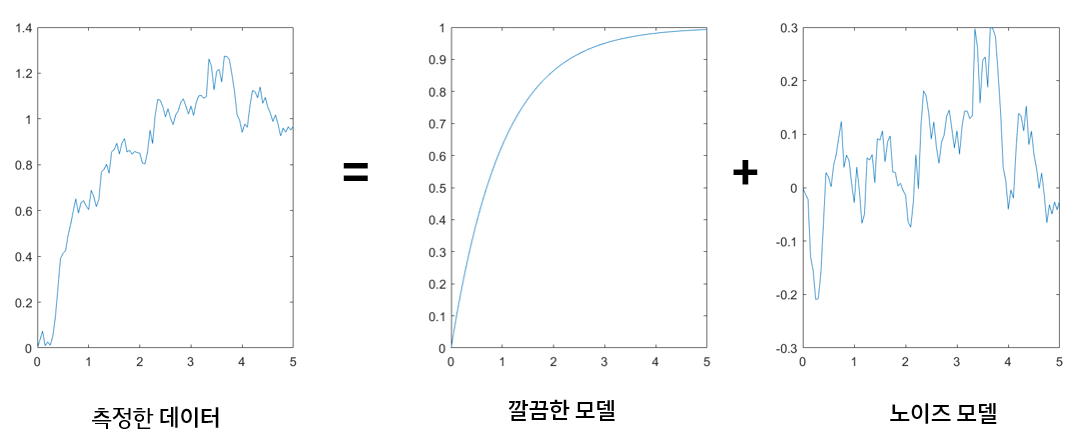
이외에도 모델을 noisy한 부분과 깔끔한 부분으로 분리해서 파악하는 stochastic model도 있습니다!
나는 샤워기에 쓰지만, 현실에서는 어디에 쓰일까?
이러한 경험적 모델링은 현재는 어디에 주로 사용되고 있을까요?
정답은 바로 모든 공정입니다!
현재의 공정은 대부분 복잡하고 커다랗기 때문에, 이론적 모델링을 하기는 거의 불가능하고 피드백 제어만으로 제어하기에도 어려움이 많습니다. 그렇게 때문에 경험적 모델링을 주로 사용합니다.
특히나 입력과 출력 사이에 시간 차가 큰 경우에는 피드백 제어가 사용하기 어렵습니다. 예를 들어 샤워기가 수도꼭지를 돌리고 30초가 지나야 이것이 반영되어 물 온도가 변한다고 해봅시다. 피드백 제어를 사용하면, 물이 차가워서 수도꼭지를 뜨거운 쪽으로 돌리지만 여전히 물이 차갑습니다. 여러분은 30초가 지나기까지 수도꼭지를 계속 더 뜨거운 쪽으로 돌릴 테고, 결과적으로 나중에는 엄청 뜨거운 물이 나옵니다. 그럼 이제는 수도꼭지를 다시 차가운 쪽으로 돌립니다. 하지만 여전히 뜨겁습니다! 결국 너무 차가운 쪽으로 많이 돌린 나머지 나중에는 얼음물이 나오겠죠. 이게 반복되면 결국 따뜻한 물은 거의 맞지 못하고 제어에 실패하게 됩니다.
또 농업 같은 경우에는, 물 주는 양을 조절해야 하는데 물을 너무 많이 주어 뿌리가 썩어버렸다고 합시다. 그러면 피드백을 통해 물 주는 양을 줄여야 겠죠? 하지만 이미 식물이 죽어서 소용이 없습니다… ㅠㅠ 이런 경우에는 피드백 제어를 하기 어렵기 때문에 경험적 모델링을 통해 미리 파악하는 것이 중요합니다.

마지막으로 Model Predictive Control을 하기 위해서는 모델을 파악해야 합니다. 이름은 어렵게 보이지만, 사실은 그냥 모델을 통해 미래를 예측해서 제어하는 방법입니다. 지금 이 상태대로 간다면 출력이 어떻게 될지 예측하고, 얼마큼 입력을 바꿔야 우리가 원하는 값으로 출력이 변할지 예상해서 조절하는 방법이니만큼, 결과를 보고 나서야 조금씩 조절하는 피드백 제어에 비해 성능은 훨씬 좋겠죠?

단점 없이 완벽한 경험적 모델링?
사실 이런 경험적 모델링에도 단점은 있습니다. 아까 말한 변기 물처럼, 우리가 조절할 수 없지만 결과에 영향을 주는 요소를 외란이라고 합니다. 경험적 모델링을 정확히 하기 위해서는 이런 외란에 대해서도 다 실험을 해주어야 합니다. 외란이 많을수록 실험을 더욱 많이 해야 하겠죠.
게다가 외란 중에는 우리가 파악할 수 없거나, 알더라도 실험을 할 수 없는 경우도 많습니다. 이런 점에서는 내부 구조를 모두 파악하고 있는 이론적 모델링에 비해 부정확도가 더욱 높아질 수밖에 없습니다.
이 정도면 됐다!

어쨌든 우리의 샤워기 예제에서는, 이 정도만 해도 충분히 마스터가 될 수 있습니다! 이제 집에 가서 몇 번만 실험하면, 평생 물 온도 조절의 장인이 될 수 있다구요! 꼭 한 번 실천해보시길 바라면서 글 마치겠습니다.
감사합니다!
Reference
[1] Seborg, D. E., et al. Process Dynamics and Control. Wiley, 2004.
[2] Yerramareddy, Sudhakar, et al. “Developing Empirical Models from Observational Data Using Artificial Neural Networks.” Journal of Intelligent Manufacturing, vol. 4, no. 1, 1993, pp. 33–41.
'STEM - 학술세미나 > 전기정보공학' 카테고리의 다른 글
| 반도체 업계 동향과 산업계 소식 (2) | 2022.12.20 |
|---|---|
| 스마트 워치들은 우리의 심박수와 호흡을 어떻게 측정하는 걸까? (2) | 2021.06.12 |
| 전자기학과 딥러닝? DNN 모델로 최적의 광학 구조 탐색하기! (0) | 2021.06.11 |




댓글