안녕하세요? 공우 14기 전기정보공학부 19학번 채범준입니다. 저는 전기정보공학부 3학년을 대상으로 봄학기에 열리는 “양자역학의 응용” 과목을 소개해 보려고 합니다.
1. 과목에서 배울 수 있는 내용
1.0. 전반적인 구성
이 과목은 반도체와 전자물리 분야의 기반을 이루는 양자역학을 공부하는 과목입니다. 내용은 크게 세 부분으로 나눌 수 있습니다. 우선 1부에서는 양자역학의 형식(formalism), 즉 양자 세계를 기술하는 파동함수 Ψ(x; t) (‘프사이’라고 읽습니다)의 의미와 이 함수가 따르는 방정식인 Schrodinger equation을 알아보고, 몇 가지 상황을 상정해 이 방정식을 풀어봅니다.
대칭적인 퍼텐셜 등 조건이 정말 간단한 경우에는 이 방정식을 손으로 풀 수 있지만, 그래도 현실이 녹록치 않은 때가 많습니다. 2부에서는 이러한 문제들을 공략할 수 있는 방법의 하나로 perturbation theory를 공부합니다. perturbation theory를 이용하면 복잡한 형태의 퍼텐셜에 대한 에너지 상태를 근사적으로 찾아내는 문제를 풀 수도 있고, 빛을 받은 전자가 에너지를 흡수해서 높은 에너지 준위로 올라가거나(Fermi’s golden rule) 빛에 의해 에너지를 방출하면서 낮은 준위로 내려가는 상황(stimulated emission)을 이해할 수 있습니다.
지금까지는 입자의 숫자가 세 개를 넘어가지 않는 문제만을 주로 다루었지만, 경우에 따라서 입자의 개수가 10의 23제곱 정도 되는 문제들을 생각해볼 수도 있습니다. 입자들의 움직임을 하나하나 추적할 수 없기에 여기에서는 통계적인 방법을 사용하게 됩니다. 3부에서는 입자의 종류에 따라서 3가지의 통계를 사용할 수 있으며, 각 입자의 성질로부터 이 통계들이 어떻게 유도되는지를 배웁니다. 이를 기반으로 해서 Planck의 blackbody radiation이나 전자의 Fermi-Dirac distribution 등의 현상을 이해할 수 있습니다.
1.1. 양자역학의 형식: 파동함수의 의미와 Schrodinger 방정식
물리학에서 하나의 주파수를 가진 파동은 사인파로 이해합니다. 하지만 이것을 삼각함수 대신 복소수 지수함수의 실수부로 생각하면 계산이 편리해지기에, 실제 정량적인 해석과 판단은 대개 복소수 상에서 이루어집니다.
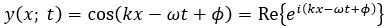
따라서 사인파 y(x; t)를 위와 같이 나타낼 수 있으며, 표기 상의 편의를 위해 실수부 기호 Re는 생략하곤 합니다.
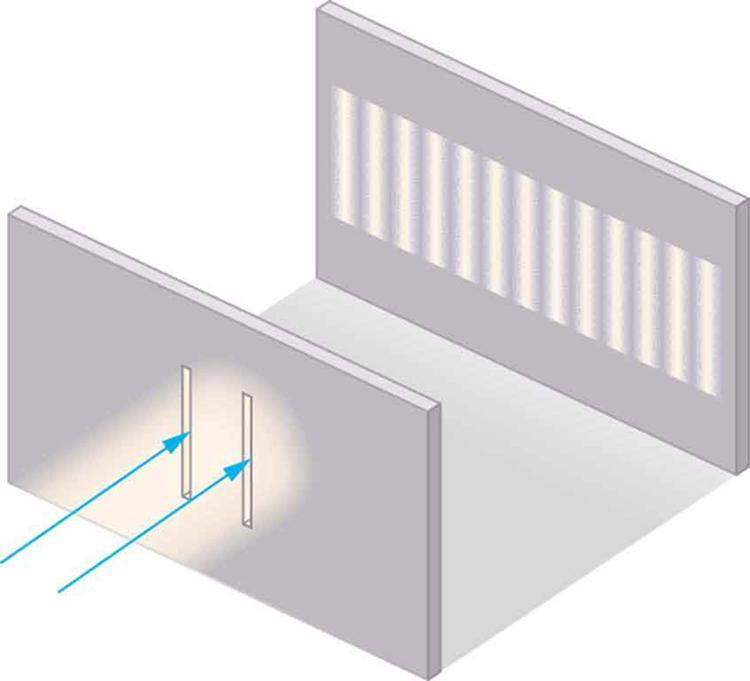
또한, 광학에서 우리 눈에 보이는 것은 field의 절댓값의 제곱에 비례하는 에너지입니다. 이것을 이용하면 [그림 1]의 Young의 이중 슬릿 실험에서 스크린에 줄무늬가 나타나는 이유를 설명할 수 있습니다. 즉, 스크린에 나타나는 줄무늬는 간섭한 두 복소수 파동의 절댓값 제곱이 됩니다.
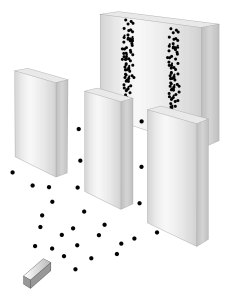
양자역학에서는 전자 같은 입자도 결국 실체는 복소수로 기술되는 파동이라고 말합니다. [그림 2]에서처럼 전자도 빛과 같이 이중 슬릿 건너편의 스크린에 줄무늬를 만들어내기 때문입니다. 이러한 파동은 Ψ(x; t)로 기술됩니다. Compton의 산란 실험과 de Broglie의 이론에 의하면 파장 λ과 운동량 p 사이에는 다음 관계가 성립합니다:
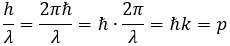
그리고 위치, 운동량, 각운동량, 에너지와 같은 입자의 물리량은 그 자체로 존재하는 것이 아닌 입자의 파동함수로부터 얻어지는 것으로 양자역학에서는 이해합니다. 그렇기에 우선 파동 Ψ(x; t)가 있고 각 물리량에 대응되는 operator가 있어서, 이 입자의 물리량은 파동함수에 operator를 적용함으로써 얻어집니다. 어떤 물리량을 A라고 하면, 이에 해당하는 operator는 A에 hat을 붙여서 나타냅니다. 따라서 파동함수에 A에 해당하는 operator를 적용해 A 값을 알아내는 것은
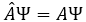
로 표현됩니다. 예를 들어, 운동량 operator는
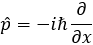
이고, +x 방향으로 나아가는 자유전자는
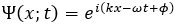
의 파동함수로 표현됩니다. 따라서
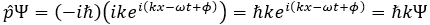
이므로 이 자유전자의 운동량은 p= ℏk가 됩니다. 이는 de Broglie 이론이 보여주는 관계와 동일합니다. 사실 이 파동함수는 운동량이 결정된 특별한(eigen) 함수입니다.
Schrodinger equation은 (상대론적 효과를 무시할 때) 입자의 파동함수가 따르는 방정식입니다:
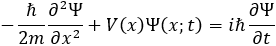
편미분방정식을 풀기 위해 가장 먼저 시도하는 방법은 두 변수 x와 t를 분리하는 것입니다(이를 Separation of Variables 방법이라고 부릅니다). 함수 Ψ(x; t)가 ψ(x)ϕ(t)의 형태로 나타난다고 가정한다면 위 방정식은
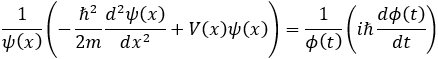
가 되므로, 결국 좌우변의 값이 상수가 됨을 알 수 있습니다. 그런데, 혹시 눈치 채셨나요? 좌변의 괄호 안에 있는 식을 다르게 써보면
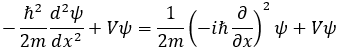
가 되므로 이는 결국

즉, 입자의 총 에너지를 나타내는 식이 됩니다. 따라서 앞서 변수분리를 적용한 식의 상수를 E로 표기하면 위 식은
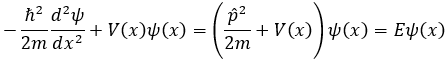
로 쓸 수 있습니다. Time-independent Schrodinger equation이라고도 불리는 이 식은, 결국 입자의 에너지 보존법칙을 나타내는 식이라고 생각할 수 있습니다.
결국 양자역학에서 입자의 상태를 파악하는 문제는 Schrodinger equation을 풀어 ψ(x)를 얻어내는 문제로 귀결됩니다. Schrodinger equation과 주어진 문제 상황의 퍼텐셜 에너지 V(x), 그리고 boundary conditions이 해당 상황에 놓인 입자의 파동함수 ψ(x)를 결정하게 됩니다. 이제 손으로 풀 수 있는 (exact solution이 존재하는) 몇 가지 상황, 가령 infinite square well, harmonic oscillator, hydrogen atom 등에 대한 문제들을 풀어보게 됩니다.
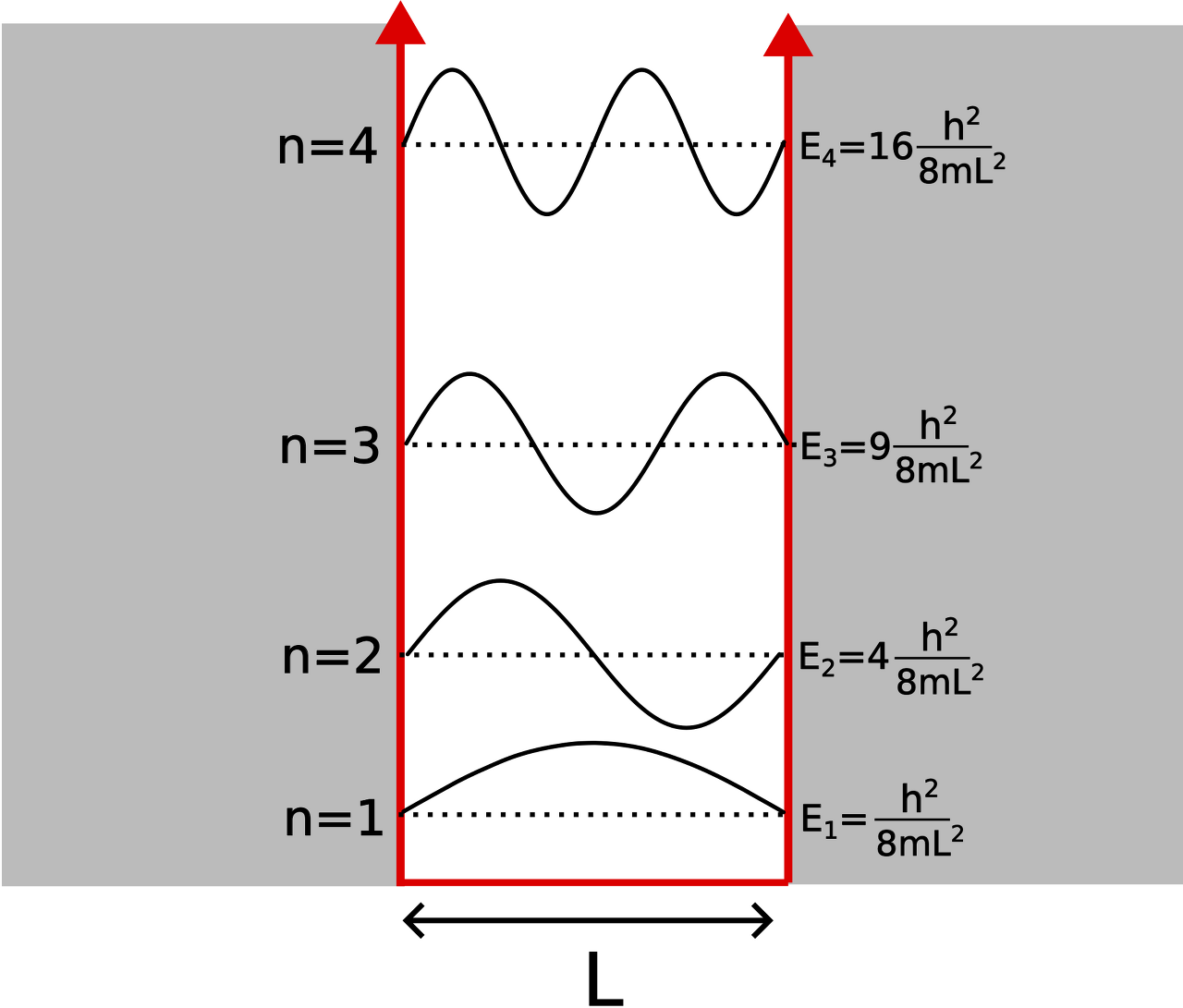
여기서는 간단하게 1차원 infinite square well 문제만 살펴봅시다. 이 상황은 퍼텐셜 V(x)가
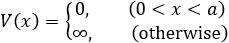
로 나타나는 상황이며, Schrodinger equation에 대입하여 방정식을 풀어내면 오직
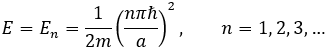
즉, E는 자연수 n과 대응되는 특정한 값만 가질 수 있게 됩니다. 이때 ψ(x)는
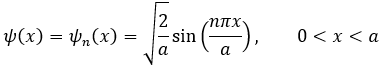
가 됩니다. 나머지 구간에서는 퍼텐셜이 ∞이므로,
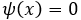
이게 됩니다. 이렇게 해서 얻어낸 solution set
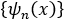
은 시스템이 정의된 구간(여기에서는 로 생각하겠습니다)에서 임의로 주어진 함수 ϕ(x)에 대해
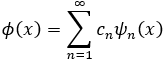
로 표현할 수 있습니다. 즉 {ψn(x)}는 함수공간의 basis로 쓸 수 있으며 이것을 “집합 {ψn(x)}이 complete하다”라고 합니다. 이는 뒤에서 풀게 될 harmonic oscillator, hydrogen atom의 solution sets도 마찬가지로 가지고 있는 성질입니다.
각각의 상황에 대해서 Schrodinger equation을 푸는 것은 지루한 작업으로 느껴질 수 있습니다. 하지만 이들 간단한 상황들은 나중에 coupled oscillator, blackbody radiation 같이 물리적으로 복잡한 문제를 쉽게 파악하는 model로 이용됩니다. 모든 식 전개를 외우기는 힘들더라도, 몇 번 연습을 통해 유도 과정을 잘 익히는 것이 좋겠습니다.
1.2. 양자역학의 응용: Perturbation Theory를 중심으로
앞에서 살펴본 infinite square well이나 harmonic oscillator, hydrogen atom 같은 문제에서는 퍼텐셜 함수가 비교적 간단한 형태를 띠고 있습니다. 하지만 실제 마주하게 되는 문제들은 퍼텐셜이 그보다 더 복잡합니다. Perturbation theory는 이렇게 복잡한 문제에 대처하는 방법 중 하나입니다. 이것은 주어진 시스템을, 기존에 답을 알고 있는 시스템에 아주 작은 교란(perturbation, 섭동이라고도 합니다)이 합쳐진 형태로 보고, 그 해를 근사적으로 구하는 방법입니다. 즉, 이 시스템을 기술하는 Hamiltonian을
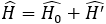
와 같이, (square well, harmonic oscillator, hydrogen atom 등) solution을 알고 있는 Hamiltonian H0와 그보다 아주 작은 (시스템에 아주 미약한 영향을 끼치는) H′ 이 둘이 합쳐진 형태로 나타내어 문제를 해결하는 것입니다.
H0에 대한 eigenstates를
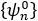
라고 표기하도록 하겠습니다. 앞에서 이러한 집합은 complete한 성질을 갖는다고 하였습니다. 즉, 이들 eigenstates를 일차결합하면 시스템의 정의역 상에서 주어지는 모든 함수들을 표현할 수 있습니다. 이제 목표는, 이 성질을 이용해서 주어진 시스템 H=H0+H′의 eigen-energy 와 eigenstate ψ를 H0의 eigenstates와 eigenenergy로 나타내는 것입니다. 즉, H의 eigenstates {ψn}와 그에 해당하는 eigenenergy를
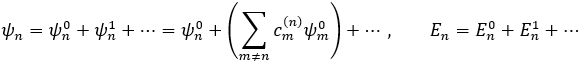
로 나타낼 때 이 식의

을 찾아야 합니다. H0는 Hermitian이기 때문에 solution set의 원소들은 서로 orthogonal하므로 이 성질을 이용하면

라는 관계를 얻어낼 수 있습니다. 이 둘은 각각 eigenstate와 eigenenergy에 대해 일차적인 보정을 진행한 것이라고 볼 수 있어요(first order correction). 더 많은 계산을 거치면 2차, 3차 보정도 얻어낼 수 있지만, 보통은 1차까지만 이용합니다.
여기까지는 퍼텐셜이 정지해 있어서 시간에 따라 변하지 않는다고 간주하였습니다, 하지만, 퍼텐셜이 시간에 따라 변하는 상황을 생각해볼 수도 있습니다. 평면파의 빛이 입사하면서 potential이 sinusoidal하게 변하는 경우가 대표적인 예시인데요, 이러한 문제를 풀 때 사용하는 방법 중 하나로 time-dependent perturbation theory가 있습니다.
앞에서 시스템의 Hamiltonian을 “답을 알고 있는 부분”과 “(답은 모르지만)그 영향이 아주 미약한 부분”으로 나누었잖아요? 비슷하게, 여기에서는 Hamiltonian을 “답을 알고 있는 부분”과 “(답은 모르지만) 그 영향이 미약하며 시간에 따라 변하는 부분” 두 가지로 나누어 생각해봅니다. 식으로 이렇게 표현할 수 있겠네요.
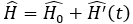
그리고 Schrodinger 방정식을 풀어서 얻는 eigenfunction set이 complete하다는 사실은 여기서도 쓰이게 됩니다. 즉, 얻으려고 하는 solution Ψ(x;t)를 H0의 eigenstates의 일차결합으로 표현하려고 합니다. Time-dependent Schrodinger equation에 따르면, 각 eigenstates는 그에 해당하는 에너지에 비례하는 주파수로 진동하게 됩니다. 따라서 구하고 싶었던 solution인 Ψ(x;t)가 t=0일 때
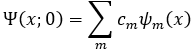
로 표현되었다면, 시간 t에서는
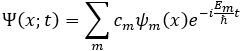
로 나타낼 수 있습니다. 사실 여기까지는 시스템이 변하지 않는 stationary한 상황에도 적용할 수 있는 방법입니다.
Time dependent perturbation theory는 위 식에서,
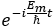
뿐만 아니라 각 항의 계수까지 시간에 따라 변하는 것으로 생각합니다. 따라서 위 식에서
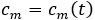
로 바꾸어
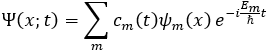
로 이해하고 이론을 전개합니다. 식의 나머지 부분은 이미 알고 있으므로, 결국 관건은 계수가 시간에 따라 어떻게 변화하는지를 찾아내는 것이라고 볼 수 있겠네요.
수식을 모두 전개하는 것은 다소 복잡하기에, 이 이론이 적용되는 유명한 예시를 두 가지 소개하고 마칠까 합니다. 우선 Fermi’s Golden Rule라는 규칙이 있습니다. 시간에 따라서 주파수 ω로 sinusoidally하게 변하는 퍼텐셜이 주어지고 그 상황에 입자가 하나 놓여 있는 상황을 생각합니다. 그러면 입자가 한 에너지 상태 ∣i⟩에서 다른 에너지 상태 ∣f⟩로 전이하게 되는데, 이 두 상태의 에너지 차이는 ℏω로 나타납니다. 여기까지는 전에 물리나 화학 시간에 배운 내용과 크게 다르지 않을 것입니다. 이제 Fermi’s Golden Rule의 핵심은, 이러한 전이가 얼마나 빠르게 나타나는지를 알려준다는 데에 있습니다. 이 규칙에 따르면, 전이가 일어나는 빠르기는 다음과 같습니다:
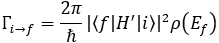
여기서 ∣⟨f∣H′∣i⟩∣는 perturbation에 의해 전이가 이루어지는 두 상태가 얼마나 잘 어울리는지를 나타내는 양이며, ρ(Ef)는 최종적으로 전이가 이루어져야 하는 에너지에 해당하는 상태가 얼마나 많은지를 나타내는 density of states입니다.
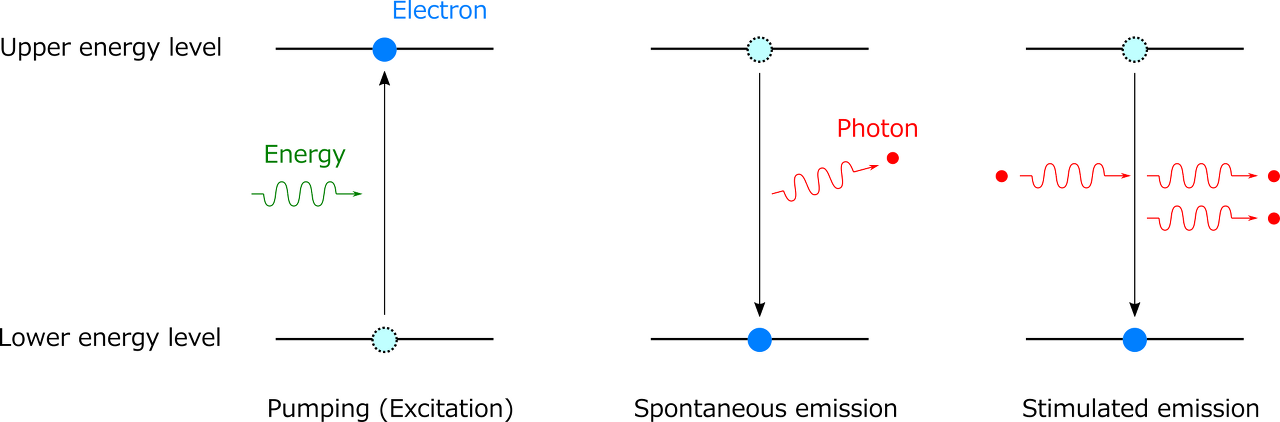
또 Einstein‘s A and B coefficients가 있는데, 사실 이 내용은 stimulated emission의 발견으로 더 유명한 것 같습니다. 간단히 두 에너지 상태를 갖는 입자를 생각해봅시다. 이전에도 언급했듯이 시간에 따라 sinusoidal하게 변하는 퍼텐셜은 평면파 형태의 빛이 입사하는 것으로 볼 수 있다고 하였습니다. 광전효과나 원자핵 주위를 도는 전자가 전이하는 것에서 볼 수 있듯, 대개 외부에서 빛이 들어오면 입자는 그 에너지를 흡수해(absorption) 낮은 에너지 상태에서 높은 에너지 상태로 올라갑니다. 반대로 높은 에너지 상태에 있다가 에너지를 빛이나 열의 형태로 “자발적으로” 방출하고(spontaneous emission) 낮은 에너지 상태로 내려올 수도 있지요. 이 둘만 생각하기 쉬운데, Einstein은 외부에서 들어온 빛이 오히려 높은 에너지 상태에 있던 입자를 내려오게 촉진할 수도 있다는 사실을 발견했습니다. 대부분의 경우(사실, thermal equilibrium을 이루고 있는 경우) 높은 에너지 상태의 입자가 낮은 상태보다 훨씬 적어서 안 보였을 뿐, 하나의 입자가 빛을 흡수하여 높은 에너지 상태로 올라갈 확률과 빛에 의해 stimulated emission를 일으켜 낮은 상태로 내려갈 확률은 B라는 계수로서 동일하게 나타난다는 것이 밝혀졌습니다(A는 나머지 하나, spontaneous emission을 결정하는 계수이겠습니다). 이 원리가 있어서 지금 우리가 레이저를 만들고 사용할 수 있게 되었습니다. 우리가 우주를 보는 관점뿐만 아니라 일상적으로 사용하고 있는 도구까지도 Einstein의 아이디어에서 출발했다는 점에서, 개인적으로 신기했던 기억이 있어요.
1.3. 더 나아가서: 통계물리 이야기
지금까지 다룬 상황에서는 대부분 입자의 개수를 다섯 손가락으로 헤아릴 수 있었습니다. 하지만 입자의 개수가 10의 23제곱에 이르면 입자 사이의 상호작용을 고려하면서 각각의 파동함수를 하나하나 찾아내기란 정말정말 어렵고 시간도 어마어마하게 걸리는 일이 될 것입니다.
이때는 입자 하나하나의 미시적인 상태를 추적하기보다는, 입자들이 구성하는 시스템의 거시적인 양을 확인하는 통계적인 기법을 사용해야 합니다. 여기서 말하는 "통계적인 기법"은, 어떠한 에너지 값이 주어졌을 때 이 에너지를 갖는 입자가 얼마나 되는지 알아내는 것을 말합니다. 그래도 시스템이 주어지면 이 시스템이 갖는 총 에너지 E와 총 입자 수 N은 알아낼 수 있으니, 결국 문제는 총 에너지 중에 에 해당하는 에너지를 갖는 입자가 전체 입자 수 N 중 얼마나 되는지 그 비율을 알아내는 것이라고 할 수 있습니다.
아원자영역의 입자는 보존과 페르미온 두 종류가 있습니다. 여기에서는 우리가 경험으로 익숙하게 접하는 고전적인 입자까지 포함하여 3가지 입자에 대해 생각하도록 하겠습니다. 우선 고전적인 입자가 여러 개 있을 때, 우리는 이 입자들을 쉽게 구별할 수 있습니다. 가령 번호가 붙은 통들을 쭉 나열해두고 입자들을 그 통 안에 집어 넣는 가짓수를 생각해본다고 하겠습니다. 일단 입자를 통에 넣은 상태에서, 두 통을 골라 그 안에 들어 있는 입자를 하나씩 꺼내 자리를 바꾼다고 하면, 이 배치는 그 이전 배치와 서로 다른 경우로 여겨지게 됩니다.
하지만 아원자 입자는 기본적으로 서로 구별할 수 없습니다. 앞의 경우에서, 두 통을 골라 그 안에 들어 있는 입자 자리를 바꾸나 그렇지 않으나 결국 같은 경우로 보아야 한다는 뜻입니다. 그리고 아원자 입자는 다시 보존(boson)과 페르미온(fermion)으로 나뉘는데요, 보존의 경우 같은 통에 입자가 여럿 들어갈 수 있지만 페르미온은 하나밖에 들어가지 못합니다.
아마 눈치챈 분도 계실 겁니다. 여기서 “통”은 입자가 가지는 “상태”를, 통에 붙은 번호는 해당 상태가 갖는 ”에너지“를 나타냅니다(물론 시스템에 따라서 degenaracy가 존재할 수도 있습니다. 이것은 같은 에너지를 갖는 여러 개의 상태가 있을 수 있다는 뜻으로, 같은 에너지에 대응되는 번호를 해당 통들에 붙인 뒤, 이들을 구별하기 위해 첨자를 하나 더 붙였다고 생각할 수 있겠습니다). 그리고 페르미온이라는 입자는 둘 이상이 동일한 상태를 점할 수 없다는 성질을 Pauli’s exclusion principle이라고 합니다. 혹시 알아차리셨나요? 전자가 바로 페르미온의 대표적인 예시입니다. 전자가 동일한 상태를 점할 수 없는 것은 이들의 같은 전하를 띠어서 서로 밀어내기 때문이 아니라, 보다 근본적인 이유(이들이 페르미온이라는 입자이기) 때문임을 알아가길 바랍니다.
이제 정량적인 분석을 하기 위해서, 총 입자 수가 N, 총 에너지가 E인 시스템을 생각해보려고 합니다. 다만 그에 앞서서, 유명한 근사식 하나를 소개하고 들어가겠습니다. Stirling approximation이라고도 불리는 이 식은 자연수 n에 대해서 ln(n!)이 아래와 같이 근사될 수 있음을 알려줍니다:
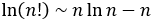
지금부터 분석을 시작하도록 하겠습니다. 자연수 i에 대하여, ϵi의 에너지에 해당하는 통이 총 개 있고, 모든 -통들에 들어간 입자 수는 이라고 하겠습니다. 그러면 다음 두 식이 성립합니다:

이제 입자를 배치하는 경우의 수 를 세어봅니다. 입자의 종류에 따라 식의 형태가 달라집니다.
(1) 고전적인 입자: 순열 개념을 사용합니다.
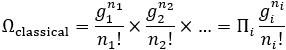
(2) 보존(Boson): 중복조합 개념을 사용합니다.

(3) 페르미온(Fermion): 일반적인 조합 개념을 사용합니다.
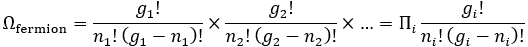
통계역학에 따르면 어떤 시스템이 열평형이 될 때 입자를 배치하는 경우의 수 가 최댓값이 된다고 합니다. 혹은, 자연로그 함수가 증가하는 함수이므로, 가 최대가 된다는 이야기는 가 최대가 된다는 뜻과 같은 의미로도 받아들일 수 있겠습니다. 여담이지만, 여기에 Boltzmann 상수 를 곱해서 로 만들면 “입자들이 배치되는 경우의 수에 로그를 취한 값”이 엔트로피라는 4글자 단어로 줄어듭니다.
결국 이 문제는 입자 개수 와 시스템의 에너지 에 대한 제약 조건 아래에서 lnΩ가 최대가 되는 상황을 구하는 문제로 바뀌게 됩니다. 즉, 상수 α와 β를 정한 뒤에 아래 식
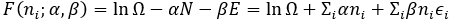
에서 F를 최적화하는 Lagrange multiplier 문제를 풀면 됩니다. 여기서는 F를 에 대해 편미분한 값만 생각하도록 하겠습니다(독립변수가 실수가 아닌 자연수이기는 합니다만, 이 이 가질 수 있는 값의 범위가 정말정말 크다면, 이 변수를 연속적인 실수 다루듯이 취급할 수 있습니다).
(1) 고전적인 입자

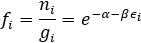
(2) 보존(Boson)
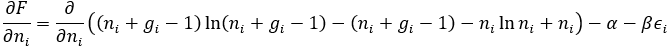
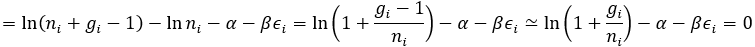
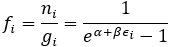
(통계역학에서 다루는 대부분의 경우 는 1보다 훨씬 큰 숫자입니다.)
(3) 페르미온(Fermion)
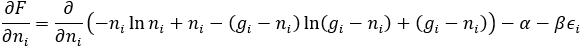
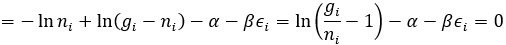
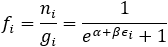
한편 α=−μ/kT, β=1/kT의 의미를 가지고 있습니다. k는 Boltzmann constant, T는 절대온도, μ는 chemical potential을 나타냅니다. 비록 여기에서는 index 를 이용하여 이산적인 변수로 식을 나타냈지만, 이들을 연속적인 변수로 생각하고 식을 써도 문제가 없습니다. 즉,
(1) Maxwell-Boltzmann Statistics (고전적인 입자가 만족하는 통계)
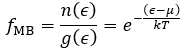
(2) Bose-Einstein Statistics (보존(Boson)이 만족하는 통계)
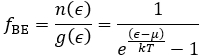
(3) Fermi-Dirac Statistics (페르미온(Fermion)이 만족하는 통계)
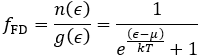
로 정리할 수 있겠습니다.
페르미온의 대표적인 예시로는 언급했듯 전자가 있습니다. Fermi-Dirac statistics는 고체의 band structure를 이해하는 기반이 됩니다. 보존의 대표적인 예시로는 광자(photon)가 있으며, Bose-Einstein statistics를 이용하면 Planck의 blackbody radiation 식을 유도할 수 있습니다.
2. 선배의 조언
이 과목은 다루는 내용이 정말 방대한 과목입니다. 자연계를 바라보는 관점을 다시 정립하는 것부터 시작하여, 선형대수학의 eigenvalue problem이 어떤 의미를 갖는지 복습하고, Schrodinger equation을 풀기 위한 여러 기법들을 익히게 됩니다. 어떤 과목을 공부하건 결국 복습과 약간의 예습이 중요합니다만, 양자역학의 경우 여러 참고 교재들을 살펴보고, 다양하게 문제도 풀어보며 전체적인 내용을 하나하나 다져나가는 것이 중요합니다.
다행(?)인 점이라고 하면, 양자역학 과목의 경우 좋은 참고 도서가 많다는 점입니다. 가장 먼저 Griffiths의 Introduction to Quantum Mechanics를 들 수 있겠습니다. 양자역학의 전반적인 내용을 하나하나 친절하게 설명해주고, 다양한 문제들을 풀면서 읽은 내용들을 충실히 복습할 수 있게 해주는 책입니다. 행여 이 수업을 듣지 않더라도 양자역학에 대해 관심이 있다면, 사 놓고 천천히 읽어보아도 좋을 것 같습니다. 무엇보다 겉표지의 고양이가 귀엽습니다.
후반에 등장하는 통계물리 내용은 Reif의 Fundamentals of Statistical and Thermal Physics 책을 참고하셔도 좋습니다. 전제조건들을 정리하면서 충실히 수식을 전개하므로, 통계물리의 개념들을 이해하고 싶다면 훌륭한 길잡이가 될 것입니다. 다만 책이 나온 지 오래 되었고 처음에는 내용이 어렵게 느껴질 수 있습니다. 저는 Schroeder의 An Introduction to Thermal Physics를 같이 보면서 공부했는데, 이 책은 통계물리 내용을 Reif에 비해 간결하게 소개하는 것이 특징입니다. 엄밀하게 내용을 정리하기 전, 공부하려고 하는 통계물리 내용이 어떻게 기술되는지 살펴볼 때 읽어보는 것을 추천합니다.
3. 진로 선택에 도움 되는 점
전기정보공학부 내에서 반도체 소자나 전자물리 분야로 진학하고자 한다면, 이 과목의 내용을 잘 숙지해야 합니다. 도체, 반도체, 유전체의 구분은 전자의 valence band와 conduction band 간 차이인 bandgap이 얼마나 되는지를 기준으로 이루어지는데, 이렇게 energy level이 둘로 쪼개지는 이유는 이들 고체가 주기적인 구조를 갖기 때문입니다. 원자가 주기적으로 배치되면 이 시스템을 나타내는 Hamiltonian은 원자 하나하나에 대한 항과 더불어, 인접한 원자들 사이에 전자가 “이동하는(hopping)" 항이 합쳐진 형태로 나타납니다. Bloch’s theorem을 적용해서 주기성을 갖는 Hamiltonian의 eigenstates를 찾을 수 있으며, 이렇게 얻은 eigenenergy가 wavevector k에 어떻게 의존하는지를 기반으로 energy band diagram을 표현할 수 있습니다. 이 diagram에서 전자가 차 있는 band와 비어 있는 band의 에너지 차이로서 bandgap을 찾을 수 있습니다.
한편, 도핑을 통해 반도체 내의 charge carrier 수를 늘리거나, 서로 다르게 도핑된 두 반도체 혹은 금속을 접합해 소자의 전기적인 특성을 조정할 수 있는데, 이들에 대한 이론적인 예측은 결국 전자의 통계역학에 그 기반을 둡니다. 아원자 입자의 통계역학은 결국 양자역학에서 출발하므로, 양자역학 지식을 쌓는 것은 반도체의 물리적 특성을 공부하는 첫걸음이라고도 할 수 있습니다.
전자물리 분야에서는 LED, 디스플레이와 같이 빛과 관련된 소자들을 개발하거나, 빛을 정보처리 혹은 통신 등에 이용하는 방법을 연구합니다. 거시적인 관점에서 빛을 파동으로 이용하고자 한다면 고전적인 전자기학과 회로이론으로도 충분하지만, light-matter interaction이나 blackbody radiation 같이 미시적인 빛의 거동을 이해하려면 결국 양자역학이 필요합니다.
전자물리 분야에서 이룩해낸 커다란 업적으로는 레이저 외에도 광섬유를 이용한 통신이 있습니다. 광섬유는 중심의 굴절률 값이 주위보다 커서, 빛이 바깥으로 새어나가지 않고 그 내부를 따라서 전파하는 원리에 기반을 두고 있습니다. 다만 섬유가 실어나를 수 있는 파동의 형태는 굴절률의 모양에 따라 하나보다 더 많을 수 있으며, 통신에 적합한 파동 형태를 얻기 위해 굴절률 모양을 인위적으로 조정해 줄 수도 있습니다. 이 과정은 결국 굴절률 값에 따라 파동 모양이 어떻게 나타나는지를 확인하는 절차가 필요한데, 재밌는 것은 굴절률이 광섬유의 빛을 결정하는 방법이 Schrodinger equation에서 퍼텐셜에 따라 시스템의 eigenstates가 정해지는 것과 수학적으로 같다는 것입니다. 꼭 양자역학 지식이 쓰이지 않더라도, 양자역학에서 쓰이는 여러 수학적인 기교는 다른 여러 문제들을 풀 때 도움을 주기도 합니다.
최근 양자정보에 대한 관심이 높아지면서, 원래 물리를 많이 다루지 않던 분야도 양자역학에 관한 지식이 조금씩 필요해지는 것 같습니다. 정보처리, 통신 혹은 보안 등의 분야에 관심이 있는 분들이라면, 수학적인 기교까지 파고들 필요는 없더라도 양자역학에서 받아들이고 가는 전제조건 혹은 파동함수의 해석 같은 형식적 측면을 주로 공부해보는 것을 추천합니다. 이 내용을 숙지한 후에 양자컴퓨터, 양자정보 및 양자암호 내용으로 들어간다면 해당 기술들이 구현되는 방식과 의미를 더욱 명확하게 이해할 수 있으리라 생각합니다.
4. 맺음말
꼭 관련 수업을 수강하지는 않더라도, 양자역학은 언제 한번 시간 내어 공부해볼 가치가 있는 과목이라고 생각합니다. 파격적으로 등장해 지금까지도 많은 논쟁을 가져오고 있지만, 한편으로는 우리가 더욱 근본적인 차원에서 자연을 이해하고 현대 기술 문명을 이룩하는 데에 기여하고 있는 학문입니다. 이 과목을 공부하면서 여러분도, 지금까지 주변을 바라보던 관점에 대해 다시 성찰해보고, 다양한 참고자료와 연습문제를 통해 양자역학의 이야기를 차근차근 곱씹어 보면서, 물리 지식 면에서나 일상을 살아가는 자세에서 한층 성장한 여러분들의 모습을 발견할 수 있으면 좋겠습니다.
Reference
[1] Griffiths, D. J., Schroeter, D. F. Introduction to Quantum Mechanics, 3rd ed, Cambridge, 2018.
[2] Yariv, A. An Introduction to Theory and Applications of Quantum Mechanics, Dover, 2013.
[3] Reif, F. Fundamentals of Statistical and Thermal Physics, Waveland, 2009.
[4] Schroeder, D. V. An Introduction to Thermal Physics, 1st ed, Oxford, 2020.
[5] Tong, D. Applications of Quantum Mechanics, 2017, https://www.damtp.cam.ac.uk/user/tong/aqm.html.

'전공백서 > 전기정보공학부' 카테고리의 다른 글
| 전기정보공학부: 논리설계 및 실험 (3) | 2023.12.28 |
|---|---|
| 전기정보공학부: 컴퓨터조직론 (2) | 2023.12.26 |
| 전기정보공학부: 지능시스템개론 (0) | 2023.12.05 |
| 전기정보공학부: 컴퓨터조직론 (1) | 2023.08.29 |
| 전기정보공학부: 컴퓨터비전의 기초 (0) | 2023.08.28 |





댓글