안녕하세요! STEM 13기 전기정보공학부 문재홍입니다.
이 글을 통해서 제가 다루어보려고 하는 주제는 다변수해석학입니다. 서울대학교 공대생이라면 누구나 1학년 때 수학 및 연습 2를 수강하시면서 스토크스 빔 한 번씩 맞아보셨을 텐데요... 여러분은 이 스토크스 정리를, 나아가서는 다변수 해석학을 얼마나 잘 이해하고 계신가요? 제가 수강하면서 궁금했던 부분들을 중심으로 이를 풀어나가보려고 합니다!
1. 다변수함수에서 미분과 적분이란?
고등학교 때 미적분학을 배운 사람에게 미분과 적분이 무엇이냐 하고 묻는다면 대부분은 아마도 '미분은 기울기고 적분은 미분의 역연산이다!'라고 답을 할 것입니다.
하지만 다변수에서는 어떨까요? $f:R^n \rightarrow R$ 과 같은 함수가 있을 때 여러분은 기울기를 어떻게 정의하실 것인가요? 그리고 적분은 미분의 역연산이라는데... 위의 연산의 역연산은 도대체 어떻게 되는 것일까요..?
$\bf{a}$ $\in R^m, f:R^m \rightarrow R^n$일 때, 우리는 다음식을 만족하는 $n \times m$ matrix를 $\textbf{a}$에서의 미분값으로 정의합니다.
$$\frac{f(\textbf{a} + \textbf{u}) - f(\textbf{a}) - B \cdot \textbf{h}}{\|\textbf{h}\|} \rightarrow 0 \quad \text{as} \quad \textbf{h} \rightarrow \textbf{0}$$
복잡해 보이는 식이지만 의미는 간단합니다. 미분은 $\textbf{a}$ 근방에서 함수값에 가장 가까운 선형 변환을 의미합니다. 테일러 시리즈를 생각해보면 이러한 미분의 정의는 우리가 기존에 알고 있던 미분과 부합하는 듯합니다!
그렇다면 적분은 무엇일까요? $f:R^n \rightarrow R$가 있을 때, $R^n$의 subset $U$ 위에서의 적분 $\int _{U} f$는 구분구적법으로 정의하게 됩니다. $U$를 조각조각 내고... 각각의 조각의 부피와 조각 위에서의 함숫값 하나를 잡아서 곱하고.. 이 곱을 다 더한 값을 극한으로 보내주면 우리가 원하는 적분값을 얻게 됩니다!

구분구적법으로 적분을 정의하다니... 참으로 피곤한 일이 아닐 수 없습니다! 그렇지만 고등학교 때 배운 내용을 곰곰이 되새겨보았을 때 구분구적법으로 적분을 했던 기억이 있는 것을 보니, 이러한 정의는 우리가 알고 있는 정의와 잘 부합하는 것 같습니다.
2. 고리의 질량
일단 적분이 무엇인지 정의하였으니 다른 주제로 넘어가 봅시다. 고리의 질량은 어떻게 계산할 수 있을까요?
물리학 1의 전형적인 문제죠! 고리 위에서 선밀도를 적분하면 됩니다. 그렇지만 고리 위에서 선밀도가 아니라 부피 밀도를 적분하면 어떻게 되나요? 우리는 3차원 공간 위의 어떠한 평면 또는 선의 질량이 0이라는 것을 (감각적으로) 알고 있습니다. 여러분은 이 사실에 대해서 의심해본적이 있으신가요? 고리 위에서 선밀도를 적분하면 0이 아닌 값이 나오지만 부피밀도를 적분하면 0이 됩니다. 똑같이 고리 위의 특정한 점에서 실수 값이 정의된 함수를 적분했을 뿐인데 말이죠... 과연 이를 어떻게 이해할 수 있을까요?
물론 이러한 질문이 무의미하다고 느끼시는 분들도 있을 수 있습니다! 이런 질문에 답을 하지 못하더라도 우리는 본능적으로 선의 질량, 면의 질량, 부피를 가지는 물체의 질량을 구분하여 적분할 수 있으니까요. 하지만 여러분들은 6차원에서 4차원 물체에 대한 적분을 본능적으로 계산할 수 있으신가요?
이를 위해서는 manifold라는 것을 정의할 필요가 있습니다. manifold의 정의는 다음과 같은데요... 뭔가 말이 많고 복잡해 보이지만 수및연 2에서 종종 언급하는 매끄러운 곡면이 manifold입니다(물론 정확히 말하면 이는 매개화된 manifold이지만... manifold와 parametrized manifold의 차이는 직접 공부해보도록 합시다!).

우리는 이 mainfold 위에서의 적분을 다음과 같이 정의할 수 있습니다.

즉, 이 manifold $\alpha:A \rightarrow R^n \space (A \subset R^i)$를 통해서 우리는 $n$ 차원 공간에서 $i$ 차원의 도형을 정의하게 됩니다. 공간에서 정의된 함수 $f$가 있을 때, 이를 '선밀도로 보기 위해서' 1차원의 manifold를 정의하는 $\alpha$의 정의역으로 보내서 적분을 하는 것이죠.
이러한 manifold 위에서의 적분이라면 우리는 6차원 공간에 있는 4차원 물체든, 75차원 공간에 있는 36차원 물체든 상관없이 적분을 할 수 있게 됩니다!
여기서 한번쯤 고민해볼 만한 지점은 우리는 이것을 '계산'한 것이 아니라 '정의'했다는 것입니다. 다시 말해 우리는 고리의 질량을 계산한 것이 아니라 1차원 manifold에서 정의된 적분값을 고리의 질량이라고 주장하는 상황인 것이죠!
여기서 그럼 다른 의문을 던져볼 수 있습니다. 그렇다면 우리가 흔히 하는 물리학에서의 일의 계산$\int \textbf{F} \cdot d\textbf{r}$, flux의 계산$\int \textbf{F} \cdot d\textbf{A}$ 등등은 무엇일까요? 이 적분도 마찬가지로 우리는 다른 방법으로 정의를 하고 우리가 의도한 의미를 갖는다고 주장할 것입니다.
3. 스토크스 정리
드디어 우리의 목표 스토크스 정리에 도달하였습니다! 이를 정확히 이해하기 위해서는 tensor와 orientation에 대한 이해가 필요한데요... 이는 굉장히 굉장히 어려운 주제이기 때문에 스킵하도록 하겠습니다...
이번 주제에서는 이해를 돕기 위해서 제가 직접 그린 그림들을 추가하였는데요. 저퀄리티이기는 하지만 이해해 도움이 될 것 같아서 사용하였습니다. 양해 부탁드립니다 ㅠㅠ
일단 boundary의 정의와 form이 무엇인지에 대해서만 간략히 설명드리려고 합니다.
manifold $M$의 boundary $\partial M$란 용어 그대로 manifold의 boundary를 말합니다. 만약 어떤 곡선(2-manifold)이 있다면 곡선의 양 끝 점(1-manifold)이 boundary가 될 것이고, 곡면(2-manifold)이 있다면 곡면의 테두리(1-manifold)가, 구(3-manifold)가 있다면 구면(2-manifold)이 boundary가 될 것입니다. 위의 예시에서 보시다싶이, k-manifold의 boundary는 (k-1)-manifold가 되게 됩니다(물론 고리와 같이 boundary가 존재하지 않는 경우도 있습니다만...).

$dx \wedge dy \wedge dz$와 같은 form(이의 경우 3-form)이라는 것이 있고, k-form $w$에 differential operator $d$를 적용시킨 $dw$는 (k+1)-form이 된다는 정도만 알아두시면 좋을 것 같습니다. 우리는 k-manifold 위에서 k-form의 적분을 정의하고, 고리의 질량에서 그랬듯이, 이 적분이 우리가 원하는 일의 적분, 플럭스의 적분 등이 된다고 주장하게 되는 것입니다!
스토크스 정리는 다음과 같습니다.

간단히 설명드리자면 k-manifold $M$과 (k-1)-form $w$가 있을 때, boundary와 differential operator를 통하여 (k-1)-manifold $\partial M$과 k-form $dw$를 얻게 되겠네요. 따라서 k-manifold $M$ 위에서 k-form $dw$의 적분과 (k-1)-manifold $\partial M$ 위에서 (k-1)-form $w$의 적분을 정의할 수 있게 되는데, 이 두 적분의 값이 같다는 것이 스토크스 정리입니다.
음... 뭔가 우리가 아는 스토크스 정리와는 상당히 다른 형태의 식이네요.. 그러나 정리 옆의 form의 변환식이 이 정리를 우리가 아는 스토크스 정리로 연결시켜 줍니다.
예시를 들어서 설명을 드리도록 하죠. 먼저 스토크스 정리입니다. 예시의 2-manifold $S$와 이의 boundary $\partial S$가 있습니다. 우리는 1-manifold $\partial S$ 위에서 1-form $w = \textbf{F} \cdot d \textbf{s}$의 적분을 계산하고자 하는데요. 표를 보니까 3-dimension에서 1-form에 differential operator를 취하는 것은 curl operator네요! 다시 말해 $dw = curl \textbf{F} \cdot d \textbf(S)$가 되게 되고 결국 우리가 아는 스토크스 정리를 얻게 됩니다.

가우스 정리도 증명해볼까요? 3-manifold $B$와 이의 boundary $\partial B$가 있습니다. 우리는 2-manifold $\partial B$ 위에서 2-form $w = \textbf{F} \cdot d \textbf(S)$의 적분을 계산하고 싶습니다. 표를 보니까 3-dimension에서 2-form에 differential operator를 취하는 것은 div operator네요! 다시 말해 $dw = div \textbf{F} dV$가 되고 가우스 정리를 얻게 됩니다!

마지막으로 potential energy 역시 스토크스 정리로 생각해볼 수 있습니다. 곡선 1-manifold $S$와 이의 boundary $\partial S$(여기에서는 곡선의 양 끝점 A, B)가 있습니다. 우리는 0-manifold $\partial S$ 위에서 0-form $w = F$의 적분을 계산하고 싶습니다. 표를 보니까 3-dimension에서 0-form에 differential operator를 취하는 것은 grad operator네요! 따라서 $dw = grad \textbf{F} \cdot d\textbf{s}$가 되고 우리가 잘 아는 potential energy에 대한 식을 얻게 됩니다!
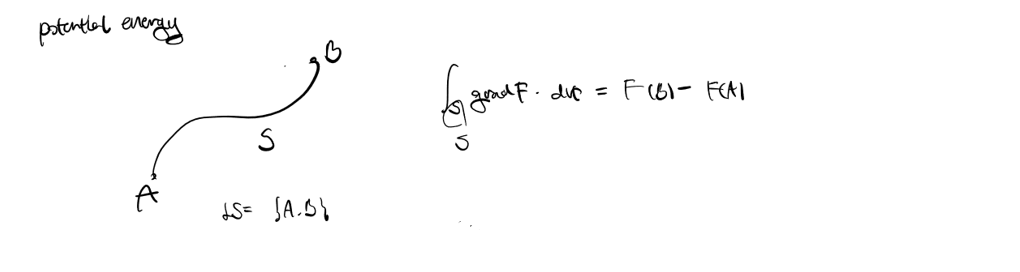
지금까지는 $R^3$에서의 스토크스 정리를 살펴보았는데요. 특히 $R^1$에서 1-manifold $S$(폐구간 $[a,b]$)과 0-form f(일변수함수)를 생각해보면 $\int_{\partial S} f = \int_{a,b} f = f(b) - f(a) = \int_{S} df = \int_{[a,b]} f'(x) dx$로 미적분학의 기본정리, 즉 '적분은 미분의 역연산이다'를 얻게 됩니다. 결국 우리는 고등학교 때부터 적분을 계산하면서 자연스럽게 스토크스 정리를 사용해왔던 것이죠!
이상으로 제가 비정기 세미나에서 다루었던 다변수 해석학에 대한 간략한 개요입니다. 이 게시글을 통해서 스토크스 정리에 대한 막연한 두려움이 해소될 수 있으면 좋겠네요! 만약 관심이 생기셔서 좀 더 엄밀하게 증명을 다루어보고 싶으신 분들께는 Munkres 선생님의 Analysis on Manifolds 책을 추천드립니다(Spivak의 Calculus on Manifolds는 제발 보지 마세요...)!
'STEM - 학술세미나 > 수학 & 통계학' 카테고리의 다른 글
| 과학과 통계학이 바꿔버린 야구 (0) | 2021.06.01 |
|---|


댓글