Welcome to Linear World!
안녕하세요! 2019년 겨울부터 다시 시작된 Stementor 프로젝트, 그 중 선형대수학 연재를 담당하게 된 공우(STEM) 10기 전기정보공학부 김경찬이라고 합니다. 반갑습니다 ^^
대다수의 공대생들에게 선형대수학은 벡터 미적분학, 미분 방정식 등과 어깨를 나란히 하는 필수적인 수학 과목인데요. 주로 1학년 때 벡터 미적분학을 배우고 나서 1학년 2학기 ~ 2학년 때 따로 수강하거나, 공학수학 시간에 배우게 되죠.
그래서 이 프로젝트는, 여러분이 기본적으로는 벡터 미적분학을 수강했고, 그래서 벡터가 무엇이고, 행렬이 무엇인지 알고 있다고 가정할게요. (아 물론 선형대수학을 이해하기 위해서 미적분학을 이해할 필요는 없습니다.)
본격적으로 시작하기 전에, 우선 선형 대수학이 무엇인지 알아보도록 할까요?
선형대수학(Linear Algebra)이란??
선형대수학이란 쉽게 말해 "선형성"이라는 성질을 갖는 대상들을 연구하는 수학의 분야라고 할 수 있습니다. 그렇다면 선형성이란 무엇일까요?
(정의) 정의역 XX의 임의의 원소 uu, vv를 공역 YY로 대응시키는 변환 TT는 다음과 같은 성질을 만족할 때 "선형 변환"이라 한다. (cc는 임의의 상수)
(1) T(cu)=cT(u)(2) T(u+v)=T(u)+T(v) (1)\ T(cu) = cT(u)\\ (2) \ T(u+v) = T(u) + T(v)
가장 쉽게 생각할 수 있는 선형 변환의 예시로는 y=axy = ax와 같이 "원점을 지나는 일차함수"가 있습니다. 이 경우 XX, YY는 실수 집합(R\mathbb{R})이 되죠.
이를 일반화시켜서, X=Rn, Y=RmX =\mathbb{R}^n,\ Y=\mathbb{R}^m인 경우를 생각해 봅시다. 이 경우는 일반적으로 다음과 같이 나타낼 수 있습니다.
y=Ax,(x∈X, y∈Y,A∈Rm×n ) \mathrm{y} = A\mathrm{x},\quad (\mathrm{x}\in X, \ \mathrm{y} \in Y, A \in \mathbb{R}^{m \times n} \ )
즉 x,y\mathrm{x, y}는 각각 n,mn, m차원의 실수벡터가 되고, AA는 m×nm \times n 실수행렬이 됩니다. 실수벡터들의 일차 변환은 행렬로 표현할 수 있는 거죠. 즉 선형대수학에서 벡터와 행렬은 가장 기본적인 재료이기 때문에 계속해서 등장합니다.
정리하자면 선형대수학은 "선형성"을 갖는 대상들을 연구하는 수학의 분야이고, 공대 학부생들은 그 중에서도 가장 기초적인 벡터와 행렬과 관련된 다양한 내용들(선형방정식, 기저, 벡터 공간, 행렬의 고윳값과 고유벡터, 행렬식 등등)을 중점적으로 공부하게 됩니다. 그런데 왜 선형대수학을 알아야 할까요?
Why Linear Algebra?
공대의 많은 학과에서 선형대수학과 관련된 과목을 듣기를 권장하거나 공학수학 교재에 등장하는 이유는, 우선 그 활용도가 매우 넓기 때문입니다. 가령 제가 재학중인 전기정보공학부에서 선형대수학과 분야들을 생각해 보면, 제어 공학, 통신 및 신호 처리, 회로 분석 등의 분야에서 행렬 연산과 행렬의 특성을 기반으로 한 시스템 해석 등을 요구합니다. 전기정보공학부를 벗어나도 공학의 온갖 분야들에서 선형적인 시스템을 다룬다거나 행렬 연산을 요구하고요.
그러나 실제 세상은 선형 시스템들로만 이루어져 있지 않죠. 자연은 물론이고, 인공적으로 만든 시스템들도 비선형적인 특징을 갖는 경우가 대부분입니다.(비선형이란 간단히 말해서 위의 선형 변환만으로 설명할 수 없는 특성을 말합니다.)
그럼에도 불구하고 우리가 선형대수학을 공부해야만 하는 이유는 비선형을 이해하기 위해서는 우선 선형을 이해해야하기 때문이에요. 실제로 비선형을 다루는 가장 초보적인, 기초적인 방법 중의 하나는 여러분이 벡터 미적분학 시간에 배운 테일러 전개의 1차항까지를 사용한 선형 근사입니다.
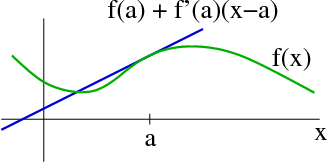
위와 같이 비선형 함수를 국소적으로 선형 함수로 근사해서 푸는 방법이죠. 이렇게 다양한 분야에서 선형 시스템을 해석하거나 높은 차원의 행렬 연산이 필요할 때, 혹은 비선형을 선형으로 근사한 뒤 해석할 때 선형대수학적 지식이 필요합니다.
또 선형대수학에서 등장하는 선형성, 벡터공간 등의 개념들은 벡터와 행렬에만 적용할 수 있는 개념이 아닙니다. 앞으로 연재 중에 관련 내용이 등장하겠지만, f(t)f(t)와 같은 연속함수들을 일종의 벡터로 볼 수 있고, 이들을 다루는 선형 변환 역시 생각할 수 있습니다. 선형대수학에서 배우는 개념들의 적용 가능 범위가 광범위하다는 것 역시 선형대수학을 배우면 좋은 이유라고 하겠습니다.
연재 계획
전반적으로는 Gilbert Strang 교수님의 "Linear Algebra and its applicaitons"의 순서를 따라갈 계획입니다. 첫 글에서는 행렬의 연산을 중점적으로 다룰 예정이고, 차근차근 나아가 최종적으로는 Singular Value Decomposition 까지를 다룰 계획입니다.
참고하면 좋은 강의
요즘은 인터넷 강의가 굉장히 발달해서 Youtube 를 통해서 MIT, Stanford 등 해외 대학의 수업을 OpenCourse 로 들을 수 있습니다. 그 중 제가 여러분께 추천하는 인터넷 강의로는 위에서 언급한 책의 저자이자 MIT 교수이신 Gilbert Strang 교수님의 OpenCourse 인 "MIT 18.06SC Linear Algebra"입니다.
해당 OpenCourse 는 인터넷 강의 뿐만 아니라 강좌와 관련된 다양한 자료들을 공개하고 있습니다. 다음의 사이트에 들어가면 해당 강의의 동영상은 물론이고 Problem Set 과 문제 풀이 동영상까지 볼 수 있습니다.
그럼 다음 글에서 뵙도록 하겠습니다. 다음 글에서는 행렬의 덧셈과 곱셈, Trace, Transpose 등의 연산에 대해 간단히 리뷰하는 시간을 갖도록 하겠습니다. 특히 행렬의 곱셈을 바라보는 다양한 방식들을 중점적으로 살펴볼게요~.
'정기연재 - 수학 & 통계학 > [선형대수학] Welcome to Linear world!' 카테고리의 다른 글
| 선형대수학_3.Vector Space (0) | 2020.02.28 |
|---|---|
| 선형대수학_2.선형방정식 Ax=b(Part1)(2) (2) | 2020.02.02 |
| 선형대수학_2.선형방정식 Ax=b(Part1)(1) (0) | 2020.01.23 |
| 선형대수학_1.행렬의 연산(2) (0) | 2020.01.01 |
| 선형대수학_1.행렬의 연산(1) (2) | 2020.01.01 |

댓글